题目内容
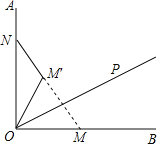
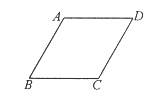
【题目】如图，M为等腰△ABD的底AB的中点，过D作DC∥AB，连结BC：AB＝8cm．DM＝4cm，DC＝1cm，动点P自A点出发，在AB上匀速运动，动点Q自点B出发，在折线BC﹣CD上匀速运动，速度均为1cm/s，当其中一个动点到达终点时，它们同时停止运动，设点P运动（s）时，△MPQ的面积为S（不能构成△MPQ的动点除外）．
（1）点Q在BC上运动时，求t的取值范围；
（2）当点Q在CD上运动时，求t为何值时，△MPQ是等腰三角形；
（3）求S与t之间的函数关系式；当t为何值时，S有最大值？最大值是多少？
【答案】（1）0＜t≤5且t≠4（s）；（2）t＝
秒；（3）当0＜t＜4时S＝﹣
t2+
；当4＜t≤5时，S＝t2﹣；当5＜t≤6时，S＝2t﹣8；当t＝6时，S取到最大值，最大值为4
【解析】
（1）过点C作CE⊥AB，垂足为E，可以证到四边形DCEM是矩形，从而可以求出BC的长，然后考虑不能构成△MPQ的情况，即可解决问题．
（2）易证QM≠MP，QP≠MP，若△MPQ是等腰三角形，只能是QM＝QP．由QF⊥MP可得：MF＝
MP．再由MF＝DQ＝6﹣t，MP＝t﹣4可得到关于t的方程，解这个方程即可解决问题．
（3）由于点P在点M的两边时PM的表达式不同，点Q在线段BC和DC上时点Q到PM的距离的表达式不同，因此需分三种情况讨论，然后只需用t的代数式表示出PM及其边上的高，就可求出S与t之间的函数关系式．利用二次函数和一次函数的性质对以上三种情况进行分析，即可解决问题
解：（1）过点C作CE⊥AB，垂足为E，如图1，
∵DA＝DB，AM＝BM，
∴DM⊥AB．
∵CE⊥AB，
∴∠CEB＝∠DMB＝90°．
∴CE∥DM．
∵DC∥ME，CE∥DM，∠DME＝90°，
∴四边形DCEM是矩形．
∴CE＝DM＝4，ME＝DC＝1．
∵AM＝BM，AB＝8，
∴AM＝BM＝4．
∴BE＝BM﹣ME＝3．
∵∠CEB＝90°，CE＝4，BE＝3，
∴CB＝5．
∵当t＝4时，点P与点M重合，不能构成△MPQ，
∴t≠4．
∴当0＜t≤5且t≠4（s）时，点Q在BC上运动；
（2）当点Q在CD上运动即5≤t≤6时，如图2，
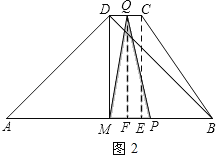
则有QM≥QF，QP≥QF，即QM≥4，QP≥4．
∵MP＝t﹣4＜6﹣4，即MP＜2，
∴QM≠MP，QP≠MP．
若△MPQ是等腰三角形，则QM＝QP．
∵QM＝QP，QF⊥MP，
∴MF＝PF＝MP．
∵MF＝DQ＝5+1﹣t＝6﹣t，MP＝t﹣4，
∴6﹣t＝（t﹣4）．
解得：t＝
．
∴当t＝秒时，△MPQ是等腰三角形．
（3）①当0＜t＜4时，点P在线段AM上，点Q在线段BC上，
过点Q作QF⊥AB，垂足为F，如图1，
∵QF⊥AB，CE⊥AB，
∴∠QFB＝∠CEB＝90°．
∴QF∥CE．
∴△QFB∽△CEB．
∴
．
∵CE＝4，BC＝5，BQ＝t，
∴
＝
．
∴QF＝
t．
∵PM＝AM﹣AP＝4﹣t，
∴S＝PMQF
＝（4﹣t）t
＝﹣
t2+
t．
②当4＜t≤5时，点P在线段BM上，点Q在线段BC上，
∵QF⊥AB，CE⊥AB，
∴∠QFB＝∠CEB＝90°．
∴QF∥CE．
∴△QFB∽△CEB．
∴．
∵CE＝4，BC＝5，BQ＝t，
∴
＝．
∴QF＝
∵PM＝AP﹣AM＝t﹣4，
∴S＝PMQF
＝（t﹣4）
＝t2﹣
．
③当5＜t≤6时，点P在线段BM上，点Q在线段DC上，
此时QF＝DM＝4．
∵PM＝AP﹣AM＝t﹣4，
∴S＝PMQF
＝（t﹣4）×4
＝2t﹣8．
综上所述：当0＜t＜4时S＝﹣t2+；当4＜t≤5时，S＝t2﹣；当5＜t≤6时，S＝2t﹣8．
①当0＜t＜4时，S＝﹣t2+t＝﹣（t﹣2）2+．
∵﹣＜0，0＜2＜4，
∴当t＝2时，S取到最大值，最大值为．
②当4＜t≤5时，S＝
t2﹣t，对称轴为x＝2．
∵＞0，
∴当x＞2时，S随着t的增大而增大．
∴当t＝5时，S取到最大值，最大值为×52﹣×5＝2．
③当5＜t≤6时，S＝2t﹣8．
∵2＞0，
∴S随着t的增大而增大．
∴当t＝6时，S取到最大值，最大值为2×6﹣8＝4．
综上所述：当t＝6时，S取到最大值，最大值为4．
