Question

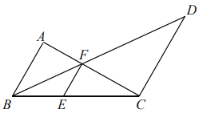
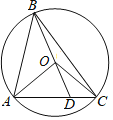
【题目】如图，已知⊙O的半径为1，AB，AC是⊙O的两条弦，且AB＝AC，延长BO交AC于点D，连接OA，OC，若AD2＝ABDC，则OD＝__．

Answer 1

【答案】．

【解析】

可证△AOB≌△AOC，推出∠ACO=∠ABD，OA=OC，∠OAC=∠ACO=∠ABD，∠ADO=∠ADB，即可证明△OAD∽△ABD；依据对应边成比例，设OD=x，表示出AB、AD，根据AD2=ABDC，列方程求解即可．

在△AOB和△AOC中，

∵AB＝AC，OB＝OC，OA＝OA，

∴△AOB≌△AOC（SSS），

∴∠ABO＝∠ACO，

∵OA＝OA，

∴∠ACO＝∠OAD，

∵∠ADO＝∠BDA，

∴△ADO∽△BDA，

∴，

设OD＝x，则BD＝1+x，

∴，

∴AD，AB，

∵DC＝AC﹣AD＝AB﹣AD，AD2＝ABDC，

（）2═（），

整理得：x2+x﹣1＝0，

解得：x或x（舍去），

因此AD，

故答案为：．