题目内容
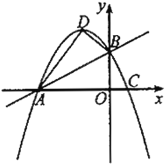
【题目】已知点P为抛物线y![]() x2上一动点,以P为顶点,且经过原点O的抛物线,记作“yp”,设其与x轴另一交点为A,点P的横坐标为m.
x2上一动点,以P为顶点,且经过原点O的抛物线,记作“yp”,设其与x轴另一交点为A,点P的横坐标为m.
(1)①当△OPA为直角三角形时,m= ;
②当△OPA为等边三角形时,求此时“yp”的解析式;
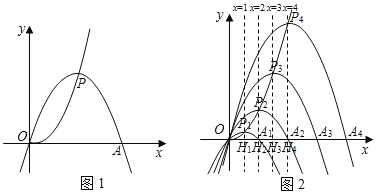
(2)若P点的横坐标分别为1,2,3,…n(n为正整数)时,抛物线“yp”分别记作“![]() ”、“
”、“![]() ”…,“
”…,“![]() ”,设其与x轴另外一交点分别为A1,A2,A3,…An,过P1,P2,P3,…Pn作x轴的垂线,垂足分别为H1,H2,H3,…Hn.
”,设其与x轴另外一交点分别为A1,A2,A3,…An,过P1,P2,P3,…Pn作x轴的垂线,垂足分别为H1,H2,H3,…Hn.
1)① Pn的坐标为 ;OAn= ;(用含n的代数式来表示)
②当PnHn﹣OAn=16时,求n的值.
2)是否存在这样的An,使得∠OP4An=90°,若存在,求n的值;若不存在,请说明理由.
【答案】(1)① 2;② y![]() x2+2
x2+2![]() x;(2)1):① (n,
x;(2)1):① (n,![]() n2);2n;② n=8;2):存在,n=10.
n2);2n;② n=8;2):存在,n=10.
【解析】
(1)①由△OPA为直角三角形时.得到△OPA为以点P为顶点的等腰直角三角形,从而可得答案,②由△OPA为等边三角形,过P作![]() 于
于![]() ,利用三角函数与抛物线的解析式
,利用三角函数与抛物线的解析式![]() ,求点
,求点![]() 的坐标,从而可得答案,
的坐标,从而可得答案,
(2)1)①利用Pn的横坐标为n,结合抛物线的对称性可得答案,②由 PnHn﹣OAn=16,建立方程求解即可,2) 画出图形,证明Rt△OP4H4∽Rt△P4AnH4即可得到答案.
解:(1)①当△OPA为直角三角形时.
∵PO=PA,故△OPA为以点P为顶点的等腰直角三角形,
∴点P的横坐标和纵坐标相同,故点P(m,m),
将点P的坐标代入y![]() x2得:m
x2得:m![]() m2,解得:m=0或2(舍去0).
m2,解得:m=0或2(舍去0).
故答案为:2;
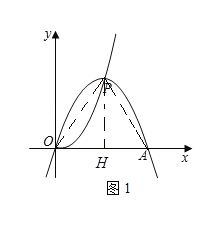
②当△OPA为等边三角形时,如图,过P作![]() 于
于![]() ,
,
![]()
![]()
![]() P(m,
P(m,![]() m),
m),
将点P的坐标代入抛物线表达式![]() ,
,
解得:m=2![]() ,
,
故点P的坐标为(2![]() ,6),
,6),
故“yp”的解析式为:y=a(x﹣2![]() )2+6,
)2+6,
点A的坐标为(2m,0),即(4![]() ,0),
,0),
将点A的坐标代入y=a(x﹣2![]() )2+6并解得:a
)2+6并解得:a![]() ,
,
故“yp”的解析式为:y![]() (x﹣2
(x﹣2![]() )2+6
)2+6![]() x2+2
x2+2![]() x;
x;
(2)1)① 由题意得:Pn的横坐标为n,则其坐标为(n,![]() n2),
n2),
由抛物线的对称性得:An=2n.
故答案为:(n,![]() n2);2n;
n2);2n;
②由题意得:PnHn﹣OAn![]() n2﹣2n=16,
n2﹣2n=16,
解得:n=8或﹣4(舍去﹣4),
∴n=8;
2)存在,理由:
如下图所示,由1)知,点P4的坐标为(4,8),An=2n,
即OH4=4,P4H4=8,H4An=2n﹣4,

∵∠OP4An=90°,∴∠OP4H4+∠H4P4An=90°.
∵∠H4P4An+∠P4AnH4=90°,
∴∠OP4H4=∠P4AnH4,
∴Rt△OP4H4∽Rt△P4AnH4,
![]()
∴P4H42=OH4H4An,
即82=4×(2n﹣4),
解得:n=10.
![]() 当
当![]() 时,使得∠
时,使得∠![]() =90°.
=90°.

 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案【题目】小李在某商场购买![]() 两种商品若干次(每次
两种商品若干次(每次![]() 商品都买) ,其中前两次均按标价购买,第三次购买时,
商品都买) ,其中前两次均按标价购买,第三次购买时,![]() 商品同时打折.三次购买
商品同时打折.三次购买![]() 商品的数量和费用如下表所示:
商品的数量和费用如下表所示:
购买A商品的数量/个 | 购买B商品的数量/个 | 购买总费用/元 | |
第一次 |
|
|
|
第二次 |
|
|
|
第三次 |
|
|
|
(1)求![]() 商品的标价各是多少元?
商品的标价各是多少元?
(2)若小李第三次购买时![]() 商品的折扣相同,则商场是打几折出售这两种商品的?
商品的折扣相同,则商场是打几折出售这两种商品的?
(3)在(2)的条件下,若小李第四次购买![]() 商品共花去了
商品共花去了![]() 元,则小李的购买方案可能有哪几种?
元,则小李的购买方案可能有哪几种?
【题目】为宣传普及新冠肺炎防治知识,引导学生做好防控.某校举行了主题为“防控新冠,从我做起”的线上知识竞赛活动,测试内容为20道判断题,每道题5分,满分100分,为了解八、九年级学生此次竞赛成绩的情况,分别随机在八、九年级各抽取了20名参赛学生的成绩.已知抽查得到的八年级的数据如下:80,95,75,75,90,75,80,65,80,85,75,65,70,65,85,70,95,80,75,80.
为了便于分析数据,统计员对八年级数据进行了整理,得到了表一:
成绩等级 | 分数(单位:分) | 学生数 |
D等 | 60<x≤70 | 5 |
C等 | 70<x≤80 | a |
B等 | 80<x≤90 | b |
A等 | 90<x≤100 | 2 |
九年级成绩的平均数、中位数、优秀率如下:(分数80分以上、不含80分为优秀)
年级 | 平均数 | 中位数 | 优秀率 |
八年级 | 77.5 | c | m% |
九年级 | 76 | 82.5 | 50% |
(1)根据题目信息填空:a= ,c= ,m= ;
(2)八年级小宇和九年级小乐的分数都为80分,请判断小宇、小乐在各自年级的排名哪位更靠前?请简述你的理由;
(3)若九年级共有600人参加参赛,请估计九年级80分以上的人数.