题目内容
【题目】如图，A（0，1），M（3，2），N（4，4）.动点P从点A出发，沿轴以每秒1个单位长的速度向上移动，且过点P的直线l：y＝－x+b也随之移动，设移动时间为t秒.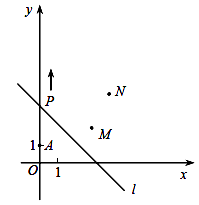
（1）当t＝3时，求l的解析式；
（2）若点M，N位于l的异侧，确定t的取值范围；
（3）直接写出t为何值时，点M关于l的对称点落在坐标轴上.
【答案】
（1）解：直线y=-x+b交y轴于点P（0，b），
由题意，得b＞0，t≥0，b=1+t．
当t=3时，b=4，
故y=-x+4．
（2）解：当直线y=-x+b过点M（3，2）时，
2=-3+b，
解得：b=5，
5=1+t，
解得t=4．
当直线y=-x+b过点N（4，4）时，
4=-4+b，
解得：b=8，
8=1+t，
解得t=7．
故若点M，N位于l的异侧，t的取值范围是：4＜t＜7．
（3）解：如图，过点M作MF⊥直线l，交y轴于点F，交x轴于点E，则点E、F为点M在坐标轴上的对称点．
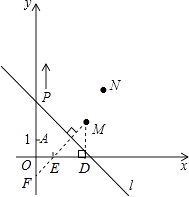
过点M作MD⊥x轴于点D，则OD=3，MD=2．
已知∠MED=∠OEF=45°，则△MDE与△OEF均为等腰直角三角形，
∴DE=MD=2，OE=OF=1，
∴E（1，0），F（0，-1）．
∵M（3，2），F（0，-1），
∴线段MF中点坐标为（ 
， 
）．
直线y=-x+b过点（ ， ），则 =- +b，解得：b=2，
2=1+t，
解得t=1．
∵M（3，2），E（1，0），
∴线段ME中点坐标为（2，1）．
直线y=-x+b过点（2，1），则1=-2+b，解得：b=3，
3=1+t，
解得t=2．
故点M关于l的对称点，当t=1时，落在y轴上，当t=2时，落在x轴上．
【解析】（1）利用直线的平移规律，上加下减，可求出解析式;(2)l令直线y=-x+b过点M、N，求出这两个临界点对应的t值，t的范围就是介于这两个值之间；（3）坐标轴包括x、y轴，分两类，利用轴对称的性质，求出t值.
