题目内容
【题目】图1所示的三棱柱,高为
,底面是一个边长为
的等边三角形.
(1)这个三棱柱有 条棱,有 个面；
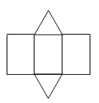
(2)图2方框中的图形是该三棱柱的表面展开图的一部分,请将它补全；
(3)要将该三棱柱的表面沿某些棱剪开,展开成一个平面图形,需剪开 条棱,需剪开棱的棱长的和的最大值为 
.
【答案】(1)9，5；(2)见解析；(3)5，31．
【解析】
(1)n棱柱有n个侧面，2个底面，3n条棱，2n个顶点；
(2)利用三棱柱及其表面展开图的特点解题；
(3)三棱柱有9条棱，观察三棱柱的展开图可知没有剪开的棱的条数是4条，相减即可求出需要剪开的棱的条数．
(1)这个三棱柱有条9棱，有个5面，
故答案为：9，5；
(2)如图（答案不唯一）；
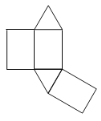
(3)由图形可知：没有剪开的棱的条数是4条，
则至少需要剪开的棱的条数是：9﹣4＝5(条)，
故至少需要剪开的棱的条数是5条，
需剪开棱的棱长的和的最大值为：7×3+5×2＝31(cm)，
故答案为：5，31．
练习册系列答案
相关题目
