Question

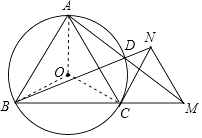
【题目】已知等边△ABC，M是边BC延长线上一点，连接AM交△ABC的外接圆于点D，延长BD至N，使得BN=AM，连接CN，MN，解答下列问题：
（1）猜想△CMN的形状，并证明你的结论；
（2）请你证明CN是⊙O的切线；
（3）若等边△ABC的边长是2，求ADAM的值．

Answer 1

【答案】
（1）解：△CMN是等边三角形，

理由：在△BCN与△ACM中， ，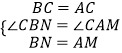

∴△BCN≌△ACM，

∴CN=CM，∠BCN=∠ACM，

∴∠BCN﹣∠ACN=∠ACM﹣∠ACN，

即∠MCN=∠ACB=60°，

∴△CMN是等边三角形

（2）解：连接OA．OB．OC，

在△BOC与△AOC中， ，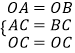

∴△BOC≌△AOC，

∴∠ACO=∠BCO= ACB=30°，

∵∠ACB=∠MCN=60°，

∴∠ACN=60°，

∴∠OCN=90°，

∴OC⊥CN，

∴CN是⊙O的切线

（3）解：∵∠ADB=∠ACB=60°，

∴∠ADB=∠ABC，

∵∠BAD=∠MAB，

∴△ABD∽△AMB，

∴ ，

∴ADAM=AB2=22=4．

【解析】（1）根据全等三角形的判定定理得到△BCN≌△ACM，由全等三角形的性质得到CN=CM，∠BCN=∠ACM，求得∠MCN=∠ACB=60°，即可得到结论；（2）根据全等三角形的性质得到∠ACO=∠BCO= ACB=30°，根据角的和差得到∠OCN=90°，根据切线的判定定理得到结论；（3）根据相似三角形的判定和性质即可得到结论．
【考点精析】掌握等边三角形的性质和三角形的外接圆与外心是解答本题的根本，需要知道等边三角形的三个角都相等并且每个角都是60°；过三角形的三个顶点的圆叫做三角形的外接圆，其圆心叫做三角形的外心．