题目内容
【题目】如图,点A的坐标为(4,0),点B从原点出发,沿y轴负方向以每秒1个单位长度的速度运动,分别以OB,AB为直角边在第三、第四象限作等腰Rt△OBE,等腰Rt△ABF,连结EF交y轴于P点,当点B在y轴上运动时,经过t秒时,点E的坐标是_____(用含t的代数式表示),PB的长是_____.
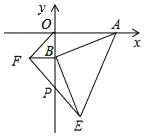
【答案】(1)(t,﹣4﹣t);(2)2.
【解析】
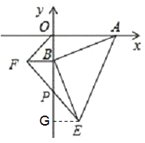 如图,作EG⊥y轴于G,
如图,作EG⊥y轴于G,
∵∠AOB=∠ABE=∠BGE=90°,
∴∠GBE+∠ABO=90°,∠BAO+∠ABO=90°,
∴∠GBE=∠BAO,
在△ABO和△BEG中,
∵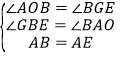 ,
,
∴△ABO≌△BEG(AAS),
∴EG=OB=t,BG=AO=4,
∴OG=OB+BG=4+t,
则E点的坐标是(t,﹣4﹣t).
∵△OBF为等腰直角三角形,
∴BF=OB,
∴BF=GE,
在△FBP和△EGP中,
∵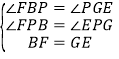 ,
,
∴△FBP≌△EGP(AAS),
∵BG=AO=4,
∴BP=GP=![]() BG=
BG=![]() ×4=2.
×4=2.
故答案为(t,﹣4﹣t);2.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案
相关题目