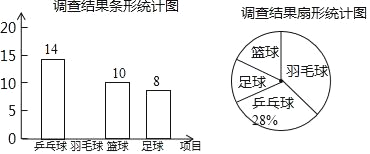
题目内容
【题目】如图，在Rt△ABC中，∠B=90°，AC=10cm，BC=6cm，现有两点P，Q分别从点A和点C同时出发，沿边AB，CB向终点B移动．其中点P，Q的速度分别为2cm/s，1cm/s，且当其中一点到达终点时，另一点也随之停止移动．设P，Q两点移动时间为x s．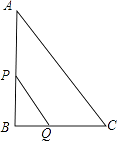
（1）用含x的代数式表示BQ、BP的长度，并求x的取值范围．
（2）设四边形APQC的面积为y（cm2），求y与x的函数关系式？
（3）是否存在这样的x，使得四边形APQC的面积是△ABC面积的 
？如果存在，求出x的值；不存在请说明理由．
【答案】
（1）
解：∵∠B=90°，AC=10，BC=6，
∴AB=8．
∴BQ=6﹣x，PB=8﹣2x
（2）
解：由题意，得
y=S四边形APQC=S△ABC﹣SPBQ
= 
ABBC﹣ PBQB
= ×6×8﹣ （6﹣x）（8﹣2x）
=24﹣（x2﹣10x+24）
=﹣x2+10x
（3）
解：假设存在x的值，使得四边形APQC的面积是△ABC面积的 
，
则﹣x2+10x= ×6×8× ，
解得x1=2，x2=8（舍去）．
假设成立，所以当x=8时，四边形APQC的面积是△ABC面积的
【解析】（1）首先运用勾股定理求出AB边的长度，然后根据路程=速度×时间，分别表示出BQ、PB的长度；（2）利用y=S四边形APQC=S△ABC﹣SPBQ求解即可；（3）根据四边形APQC的面积=△ABC的面积﹣△PBQ的面积，列出方程，根据解的情况即可判断．
【考点精析】认真审题，首先需要了解三角形的面积(三角形的面积=1/2×底×高)．
练习册系列答案
相关题目
