Question

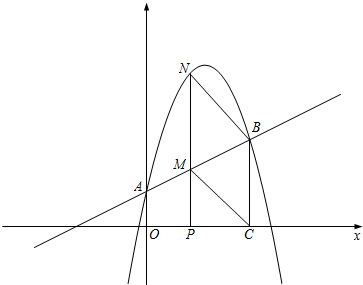
如图，已知抛物线y=

1

6

x²-

1

6

（b+1）x+

b

6

（b是实数且b＞2）与x轴的正半轴分别交于点A、B（点A位于点B的左侧），与y轴的正半轴交于点C．若在第一象限内存在点P，使得四边形PCOB的面积等于7

2

b，且△PBC是以点P为直角顶点的等腰直角三角形．求：
（1）点A的坐标为______．
（2）求符合要求的点P坐标为______．

Answer 1

（1）对于y=

1

6

x²-

1

6

（b+1）x+

b

6

，
令y=0，得到

1

6

x²-

1

6

（b+1）x+

b

6

=0，即x²-（b+1）x+b=0，
分解因式得：（x-1）（x-b）=0，
解得：x=1或x=b，
∵A在B的左边，
∴A（1，0），B（b，0）；
（2）过P作PE⊥x轴，过C作CD⊥PE，
对于y=

1

6

x²-

1

6

（b+1）x+

b

6

，
令x=0，得到y=

b

6

，即OC=

b

6

，
∵△BCP为等腰直角三角形，
∴PC=PB，∠CPB=90°，
∴∠CPD+∠BPE=90°，
∵∠CPD+∠PCD=90°，
∴∠BPE=∠PCD，
在△CDP和△PEB中，

∠PDC=∠BEP=90° ∠PCD=∠BPE PC=PB

，
∴△CDP≌△PEB（AAS），
∴CD=PE，
设P（x，x），则有CD=PE=x，
∵S_{四边形OCPB}=S_梯形OCPE+S_△PEB=

1

2

x（

b

6

+x）+

1

2

x（b-x）=7

2

b，
整理得：7x=84

2

，
解得：x=12

2

，
则P（12

2

，12

2

）．
故答案为：（1）A（1，0）；（2）P（12

2

，12

2

）