题目内容
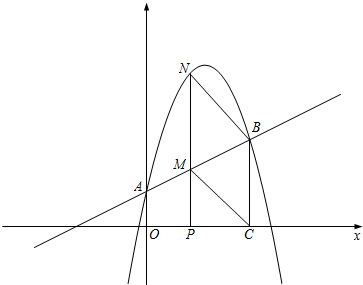
如图,抛物线y=-
x2+
x+1与y轴交于A点,过点A的直线与抛物线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0)
(1)求直线AB的函数关系式;
(2)动点P在线段OC上从原点出发以每秒一个单位的速度向C移动,过点P作PN⊥x轴,交直线AB于点M,交抛物线于点N.设点P移动的时间为t秒,MN的长度为s个单位,求s与t的函数关系式,并写出t的取值范围;
(3)设在(2)的条件下(不考虑点P与点O,点C重合的情况),连接CM,BN,当t为何值时,四边形BCMN为平行四边形?问对于所求的t值,平行四边形BCMN是否菱形?请说明理由.
| 5 |
| 4 |
| 17 |
| 4 |
(1)求直线AB的函数关系式;
(2)动点P在线段OC上从原点出发以每秒一个单位的速度向C移动,过点P作PN⊥x轴,交直线AB于点M,交抛物线于点N.设点P移动的时间为t秒,MN的长度为s个单位,求s与t的函数关系式,并写出t的取值范围;
(3)设在(2)的条件下(不考虑点P与点O,点C重合的情况),连接CM,BN,当t为何值时,四边形BCMN为平行四边形?问对于所求的t值,平行四边形BCMN是否菱形?请说明理由.

(1)∵当x=0时,y=1,
∴A(0,1),
当x=3时,y=-
×32+
×3+1=2.5,
∴B(3,2.5),
设直线AB的解析式为y=kx+b,
则:
,
解得:
,
∴直线AB的解析式为y=
x+1;
(2)根据题意得:s=MN=NP-MP=-
t2+
t+1-(
t+1)=-
t2+
t(0≤t≤3);
(3)若四边形BCMN为平行四边形,则有MN=BC,此时,有-
t2+
t=
,
解得t1=1,t2=2,
∴当t=1或2时,四边形BCMN为平行四边形.
①当t=1时,MP=
,NP=4,故MN=NP-MP=
,
又在Rt△MPC中,MC=
=
,故MN=MC,此时四边形BCMN为菱形,
②当t=2时,MP=2,NP=
,故MN=NP-MP=
,
又在Rt△MPC中,MC=
=
,故MN≠MC,此时四边形BCMN不是菱形.
∴A(0,1),
当x=3时,y=-
| 5 |
| 4 |
| 17 |
| 4 |
∴B(3,2.5),
设直线AB的解析式为y=kx+b,
则:
|
解得:
|
∴直线AB的解析式为y=
| 1 |
| 2 |
(2)根据题意得:s=MN=NP-MP=-
| 5 |
| 4 |
| 17 |
| 4 |
| 1 |
| 2 |
| 5 |
| 4 |
| 15 |
| 4 |
(3)若四边形BCMN为平行四边形,则有MN=BC,此时,有-
| 5 |
| 4 |
| 15 |
| 4 |
| 5 |
| 2 |
解得t1=1,t2=2,
∴当t=1或2时,四边形BCMN为平行四边形.
①当t=1时,MP=
| 3 |
| 2 |
| 5 |
| 2 |
又在Rt△MPC中,MC=
| MP2+PC2 |
| 5 |
| 2 |
②当t=2时,MP=2,NP=
| 9 |
| 2 |
| 5 |
| 2 |
又在Rt△MPC中,MC=
| MP2+PC2 |
| 5 |

练习册系列答案
相关题目