题目内容
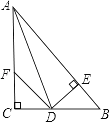
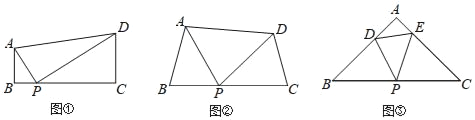
【题目】如图①,在四边形ABCD中,AB∥CD,∠B=90°,点P在BC边上,当∠APD=90° 时,可知△ABP∽△PCD.(不要求证明)
(1)探究:如图②,在四边形ABCD中,点P在BC边上,当∠B=∠C=∠APD时,求证:△ABP∽△PCD.
(2)拓展:如图③,在△ABC中,点P是边BC的中点,点D、E分别在边AB、AC上若∠B=∠C=∠DPE=45°,BC=8![]() ,CE=6,则DE的长为 .
,CE=6,则DE的长为 .
【答案】(1)证明见解析;(2)![]()
【解析】【试题分析】(1)根据两角对应相等,两三角形相似证明;(2)根据相似三角形的性质求解.
【试题解析】
∵∠APD=90°,
∴∠APB+∠DPC=90°,
∵∠B=90°,
∴∠APB+∠BAP=90°,
∴∠BAP=∠DPC,
∵AB∥CD,∠B=90°,
∴∠C=∠B=90°,
∴△ABP∽△DCP.
(1)探究:∵∠APC=∠BAP+∠B,∠APC=∠APD+∠CPD,
∴∠BAP+∠B=∠APD+∠CPD.
∵∠B=∠APD,
∴∠BAP=∠CPD.
∵∠B=∠C,
∴△ABP∽△PCD,
(2)拓展:同探究的方法得出,△BDP∽△CPE,
∴![]() ,
,
∵点P是边BC的中点,
∴BP=CP=4![]() ,
,
∵CE=6,
∴![]() ,
,
∴BD=![]() ,
,
∵∠B=∠C=45°,
∴∠A=180°﹣∠B﹣∠C=90°,
即AC⊥AB且AC=AB=8,
∴AD=AB﹣BD=8﹣![]() =
=![]() ,AE=AC﹣CE=2,
,AE=AC﹣CE=2,
在Rt△ADE中,DE=![]() =
=![]() .
.
故答案是: ![]() .
.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案
相关题目