Question

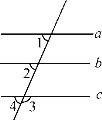
【题目】如图，已知∠1＝68°，∠2＝68°，∠3＝112°.在下列解答中，填空：

(1)因为∠1＝68°，∠2＝68°(已知)，

所以__________(等量代换)．

所以____∥_____________________________．

(2)因为∠3＋∠4＝180°(邻补角的定义)，∠3＝112°

，所以____________

又因为∠2＝68°，

所以___________(等量代换)，

所以____∥_________________________________．

Answer 1

【答案】 ∠1＝∠2 a b 同位角相等，两直线平行 ∠4＝68° ∠2＝∠4 b c 同位角相等，两直线平行

【解析】

(1)因为∠1和∠2是直线a和直线b被第三条直线所截的同位角,且∠1＝68°,

∠2＝68°,根据同位角相等,两直线平行可得:a//b,

(2)因为∠4和∠3是邻补角,所以∠4=180°-∠3,即∠4=68°, 因为∠2和∠4是直线b和直线c被第三条直线所截的同位角,且∠2＝∠4,根据同位角相等,两直线平行可得: b//c.

(1)因为∠1＝68°,∠2＝68°(已知),

所以∠1＝∠2 (等量代换)．

所以a//b, 同位角相等,两直线平行,

(2)因为∠3＋∠4＝180°(邻补角的定义),∠3＝112°,

所以∠4＝68°,

又因为∠2＝68°,

所以∠2＝∠4 (等量代换),

所以b//c同位角相等,两直线平行.

故答案为:∠1＝∠2, a ,b , 同位角相等,两直线平行, ∠4＝68°, ∠2＝∠4 ,b ,c ,

同位角相等,两直线平行.