题目内容
【题目】如图,已知抛物线与y轴交于点C(0,3),与x轴交于点A、B,点A在点B的左边,且B(3,0),AB=2
(1)求该抛物线的函数关系式;
(2)如果抛物线的对称轴上存在一点P,使得△APC的周长最小,求此时P点的坐标,并求出△APC周长;
(3)设D为抛物线上一点,E为对称轴上一点,若以点A、B、D、E为顶点的四边形是平行四边形,求点D的坐标.

【答案】(1) y=![]() ﹣4x+3 ;(2) 点P(2,1)时,△APC的周长最小,最小值为
﹣4x+3 ;(2) 点P(2,1)时,△APC的周长最小,最小值为![]() ;(3) (0,3)或(4,3)或(2,﹣1).
;(3) (0,3)或(4,3)或(2,﹣1).
【解析】
试题分析:(1)先求出点A的坐标,根据两点式设出抛物线解析式,用待定系数法求出抛物线解析式;
(2)由点A,B关于抛物线对称轴对称,所以连接BC与抛物线对称轴的交点就是点P,根据两点间的距离公式求出各线段,即可;
(3)①AB为平行四边形的边时,就有AB∥DE,AB=DE,设出点D坐标,表示出点E坐标,由AB=DE求出点D坐标;
②AB为平行四边形的对角线时,AB,DE互相平分,而点E在抛物线对称轴上,得出点D也在抛物线对称轴上,即点D就是抛物线的顶点.
试题解析:(1)∵抛物线与x轴交于点A、B,点A在点B的左边,且B(3,0),AB=2,
∴A(1,0),
设抛物线解析式为y=a(x﹣1)(x﹣3),
∵点C在抛物线上,
∴3=a×(﹣1)×(﹣3)=3a,
∴a=1,
∴抛物线解析式为y=(x﹣1)(x﹣3)=![]() ﹣4x+3,
﹣4x+3,
(2)如图1,
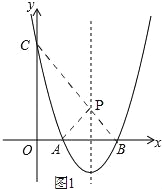
由(1)有,抛物线解析式为y=(x﹣1)(x﹣3)=![]() ﹣4x+3,
﹣4x+3,
∴抛物线的对称轴为x=2,
连接BC,交对称轴于点P,连接AP,
∵点A与点B关于对称轴对称,
∴点P就是使得△APC的周长最小时,对称轴上的点,即:PA=PB,
∵B(3,0),C(0,3),
∴直线BC解析式为y=﹣x+3,BC=![]() ,
,
当x=2时,y=1,
∴P(2,1),
∵A(1,0),
∴AP=![]() ,
,
∴△APC周长=AC+AP+CP=AC+BC=![]() +
+![]() =
=![]() ,
,
即:点P(2,1)时,△APC的周长最小,最小值为![]() ;
;
(3)∵以点A、B、D、E为顶点的四边形是平行四边形,
∴分AB为对角线和边两种情况计算,
①当AB为平行四边形的边时,AB∥DE,AB=DE,
∵点D在抛物线上,
∴设点D(m,![]() ﹣4m+3),
﹣4m+3),
∵点E在抛物线对称轴x=2上,
∴点E(2,![]() ﹣4m+3),
﹣4m+3),
∵DE∥AB,
∴DE=|m﹣2|,
∵AB=DE,AB=2,
∴|m﹣2|=2,
∴m=0,或m=4,
∴D(0,3)或(4,3),
②当AB为平行四边形的对角线时,AB与DE互相平分,
∵点E在抛物线对称轴上,
∴点D也在抛物线的对称轴上,
即:点D就是抛物线的顶点,
由(1)得,抛物线解析式为y=(x﹣1)(x﹣3),
∴抛物线顶点坐标为(2,﹣1),
∴满足条件的点D的坐标为(0,3)或(4,3)或(2,﹣1).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
