题目内容
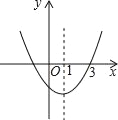
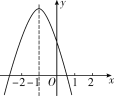
【题目】二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=-1,有以下结论:①abc>0;②4ac<b2;③2a+b=0;④a-b+c>0.其中正确的结论的个数是( )
A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】
观察图象,可得出a,b和c的符号,就可判断①是否正确;根据一元二次方程与二次函数和x轴交点之间的关系就可对②作出判断;根据对称轴是直线x=-1,就可对③④作出判断.
①∵抛物线开口方向向下,∴a<0.
∵对称轴为直线![]() ∴b=2a<0.
∴b=2a<0.
∵抛物线与y轴的交点在x轴上方,∴c>0.
∴abc>0,故①正确;
②∵抛物线与x轴有两个交点,
∴△=b2-4ac>0.
故②正确;
③∵b=2a,
∴2a-b=0.
故③错误;
④当x=-1时,根据对称性得到:y>2,即a-b+c>2.
故④正确;
综上所述,正确的结论是①②④.
故选:C.

练习册系列答案
相关题目
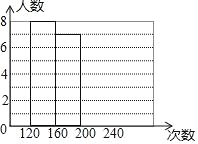
【题目】某体育老师随机抽取了九年级甲、乙两班部分学生进行一分钟跳绳的测试,并对成绩进行统计分析,绘制了频数分布表和统计图,请你根据图表中的信息完成下列问题:
分组 | 频数 | 频率 |
第一组(0≤x<120) | 3 | 0.15 |
第二组(120≤x<160) | 8 | a |
第三组(160≤x<200) | 7 | 0.35 |
第四组(200≤x<240) | b | 0.1 |
(1)频数分布表中a=____,b=_____,并将统计图补充完整;
(2)如果该校九年级共有学生360人,估计跳绳能够一分钟完成160或160次以上的学生有多少人?
(3)已知第一组中有两个甲班学生,第四组中只有一个甲班学生,老师随机从这两个组中各选一名学生谈测试体会,则所选两人正好都是甲班学生的概率是多少?