题目内容
【题目】定义：三边长和面积都是整数的三角形称为“整数三角形”.
数学学习小组的同学从32根等长的火柴棒（每根长度记为1个单位）中取出若干根，首尾依次相接组成三角形，进行探究活动.
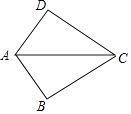
小亮用12根火柴棒，摆成如图所示的“整数三角形”；
小颖分别用24根和30根火柴棒摆出直角“整数三角形”；
小辉受到小亮、小颖的启发，分别摆出三个不同的等腰“整数三角形”.
⑴请你画出小颖和小辉摆出的“整数三角形”的示意图；
⑵你能否也从中取出若干根，按下列要求摆出“整数三角形”，如果能，请画出示意图；如果不能，请说明理由.
①画出等边“整数三角形”；
②摆出一个非特殊（既非直角三角形，也非等腰三角形）“整数三角形”.
【答案】（1）见解析;（2）见解析.
【解析】（1）利用勾股定理求出6，8，10和5，12，13符合要求，即可得出答案．
（2）首先设等边三角形的边长为a，则等边三角形的面积为
a2，进而求出不存在等边“整数三角形”.
解：⑴小颖摆出的“整数三角形”如下图所示：
小辉摆出三个不同的等腰“整数三角形”如下图所示：
每摆出一个1分，共5分
⑵①不能摆出等边“整数三角形”.理由如下：
设等边三角形的边长为a，则等边三角形面积为
.
因为，若边长a为整数，那么面积
一定非整数.
所以不存在等边“整数三角形”. …9分
②能摆出如图下图所示一个非特殊“整数三角形”：
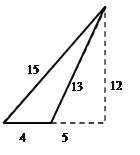
“点睛”此题主要考查了作图-应用与设计作图，等腰三角形的性质和勾股定理的应用，根据已知熟练利用勾股定理求出勾股数是解题关键．
练习册系列答案
相关题目
