题目内容
如图,在矩形ABCD中,AB=4,AD=2,点P、Q均以相同的速度同时从点A出发,点P沿AB的方向运动,点Q沿ADC的方向运动,当点P运动到点B时,P、Q同时停止运动,以PQ为一边向 上作正方形PQGH,设AP=x,正方形PQGH和矩形ABCD重合部分的面积为y,回答下列问题:
上作正方形PQGH,设AP=x,正方形PQGH和矩形ABCD重合部分的面积为y,回答下列问题:
(1)当点G在CD上时,x=
(2)求y与x的函数关系式;
(3)当x为何时时,y取最大值.
 上作正方形PQGH,设AP=x,正方形PQGH和矩形ABCD重合部分的面积为y,回答下列问题:
上作正方形PQGH,设AP=x,正方形PQGH和矩形ABCD重合部分的面积为y,回答下列问题:(1)当点G在CD上时,x=
1
1
,当点Q和点D重合时,x=2
2
;(2)求y与x的函数关系式;
(3)当x为何时时,y取最大值.
分析:(1)当点G在CD上时,证明Rt△DQG≌Rt△AQP,求出AQ,即可得出x的值.当点Q和点D重合时,AP=AQ=AD=2.
(2)分三种情况讨论,①0<x≤1,②1<x≤2,③当2<x≤4,分别画出图形,得出重合部分的面积表达式,从而可得y与x的函数关系式;
(3)根据(2)所画的图形或利用二次函数的最值即可作出判断.
(2)分三种情况讨论,①0<x≤1,②1<x≤2,③当2<x≤4,分别画出图形,得出重合部分的面积表达式,从而可得y与x的函数关系式;
(3)根据(2)所画的图形或利用二次函数的最值即可作出判断.
解答:解:(1)当点G在CD上时,如图所示:
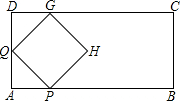
设AP=x,则AQ=x,
∴∠AQP=∠APQ=45°,
∴∠DQG=∠DGQ=45°,
在Rt△DQG和Rt△AQP中,
,
∴Rt△DQG≌Rt△AQP,
∴AQ=DQ,
又∵AD=2,
∴AQ=1,
∴AP=1.即x=1;
当点Q和点D重合时,AP=AQ=AD=2,即x=2.
(2)①当0<x≤1时,AP=AQ=x,QP=
x,
此时重合部分的面积为正方形PQGH的面积y=2x2(0<x≤1).
②当1<x≤2时,如图1所示:
∵Q'G'=P'Q'=
x,Q'N=
DQ'=
(2-x)=2
-
x,
∴G'N=Q'G'-Q'N=
x-(2
-
x)=2
x-2
∴重合部分的面积为S正方形G'Q'P'H'-S△G'MN=(
x)2-(2
x-2
)2=-6x2+16x-8;
③当2<x≤4时,如图2所示:
DQ=
x-2,AP=x,BP=BE=4-x,
∴S重合=S长方形ABCD-S△BPE-S梯形APQD=8-
(4-x)2-
(
x-2+x)×2=-
x2+(3-
)x+2;

(3)根据(2)所画图形可得,当点Q与点D重合时,重合部分的面积最大,此时x=2.

设AP=x,则AQ=x,
∴∠AQP=∠APQ=45°,
∴∠DQG=∠DGQ=45°,
在Rt△DQG和Rt△AQP中,
|
∴Rt△DQG≌Rt△AQP,
∴AQ=DQ,
又∵AD=2,
∴AQ=1,
∴AP=1.即x=1;
当点Q和点D重合时,AP=AQ=AD=2,即x=2.
(2)①当0<x≤1时,AP=AQ=x,QP=
| 2 |
此时重合部分的面积为正方形PQGH的面积y=2x2(0<x≤1).
②当1<x≤2时,如图1所示:
∵Q'G'=P'Q'=
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
∴G'N=Q'G'-Q'N=
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
∴重合部分的面积为S正方形G'Q'P'H'-S△G'MN=(
| 2 |
| 2 |
| 2 |
③当2<x≤4时,如图2所示:
DQ=
| 2 |
∴S重合=S长方形ABCD-S△BPE-S梯形APQD=8-
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |

(3)根据(2)所画图形可得,当点Q与点D重合时,重合部分的面积最大,此时x=2.
点评:本题考查了相似形的综合,解答本题的关键点在于找到几个特殊位置,①点G在CD上时,点Q运动到AD的中点,②点Q与点D重合时,点H和点C重合,注意画出每一阶段的图形,难度较大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在矩形ABCD中,AB=4cm,BC=8cm,点P从点A出发以1cm/s的速度向点B运动,点Q从点B出发以2cm/s的速度向点C运动,设经过的时间为xs,△PBQ的面积为ycm2,则下列图象能反映y与x之间的函数关系的是( )
如图,在矩形ABCD中,AB=4cm,BC=8cm,点P从点A出发以1cm/s的速度向点B运动,点Q从点B出发以2cm/s的速度向点C运动,设经过的时间为xs,△PBQ的面积为ycm2,则下列图象能反映y与x之间的函数关系的是( )



 .
. 动过程中,Q点停留了1s,图②是P、Q两点在折线AB-BC-CD上相距的路程S(cm)与时间t(s)之间的函数关系图象.
动过程中,Q点停留了1s,图②是P、Q两点在折线AB-BC-CD上相距的路程S(cm)与时间t(s)之间的函数关系图象. 如图,在矩形ABCD中,对角线AC,BD相交于点O,∠AOB=60°,AB=6,则AD=( )
如图,在矩形ABCD中,对角线AC,BD相交于点O,∠AOB=60°,AB=6,则AD=( ) DE,EF与AB交于点F,设CE=x,BF=y.
DE,EF与AB交于点F,设CE=x,BF=y.