题目内容
【题目】如图,在ΔABC中,AC=15,BC=18,sinC=![]() ,D是AC上一个动点(不运动至点A,C),过D作DE∥BC,交AB于E,过D作DF⊥BC,垂足为F,连结BD,设CD=x.
,D是AC上一个动点(不运动至点A,C),过D作DE∥BC,交AB于E,过D作DF⊥BC,垂足为F,连结BD,设CD=x.
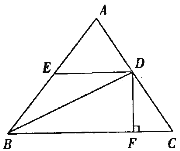
(1)用含x的代数式分别表示DF和BF;
(2)如果梯形EBFD的面积为S,求S关于x的函数关系式;
(3)如果△BDF的面积为S1,△BDE的面积为S2,那么x为何值时,S1=2S2
【答案】(1)DF=![]() x;
x;![]() ;(2)S
;(2)S![]() ;(3)x=10
;(3)x=10
【解析】
(1)可在Rt△CFD中,根据CD的长和∠C的正弦函数表示出DF,用勾股定理表示出CF,从而得出BF=BC-CF;
(2)本题中(1)已经表示出了BF,DF的长,那么关键是DE的长,可通过DE∥BC,根据平行线分线段成比例定理,得出关于AD,AC,DE,BC的比例关系式,然后根据BC的长,用x表示出DE,根据梯形的面积公式即可得出关于S与x的函数关系式;
(3)△BDF中BF,DF已经在(1)中得出,梯形的面积也在(2)中得出,可根据题中给出的它们的比例关系,得出关于x的方程,然后通过解方程即可求出x的值.
解:(1)在Rt△CFD中,sinC=![]() ,CD=x
,CD=x
∴DF=CD![]() sinC=
sinC=![]() x
x
∴CF=![]()
∴BF=18-![]()
(2)∵DE∥BC
∴![]()
∴DE=![]()
∴S=![]() ×DF×(DE+BF)=
×DF×(DE+BF)=![]() ×
×![]() x×(
x×(![]() +18-
+18-![]() )=
)=![]()
(3)由S1=2S2,得S1=![]() S
S
∴![]() (18-
(18-![]() )
)![]()
![]() x=
x=![]() (
(![]() )
)
解得![]()
∴当![]() 时,S1=2S2.
时,S1=2S2.
故答案为(1)DF=![]() x;
x;![]() ;(2)S
;(2)S![]() ;(3)x=10
;(3)x=10

 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案【题目】某商场有一个可以自由转动的圆形转盘(如图).规定:顾客购物100元以上可以获得一次转动转盘的机会,当转盘停止时,指针落在哪一个区域就获得相应的奖品(指针指向两个扇形的交线时,当作指向右边的扇形).下表是活动进行中的一组统计数据:

转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
落在“铅笔”的次数m | 68 | 111 | 136 | 345 | 546 | 701 |
落在“铅笔”的频率 (结果保留小数点后两位) | 0.68 | 0.74 | 0.68 | 0.69 | 0.68 | 0.70 |
(1)转动该转盘一次,获得铅笔的概率约为_______;(结果保留小数点后一位)
(2)铅笔每只0.5元,饮料每瓶3元,经统计该商场每天约有4000名顾客参加抽奖活动,请计算该商场每天需要支出的奖品费用;
(3)在(2)的条件下,该商场想把每天支出的奖品费用控制在3000元左右,则转盘上“一瓶饮料”区域的圆心角应调整为______度.