Question

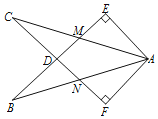
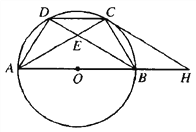
【题目】如图，点A、B、C、D是直径为AB的⊙O上的四个点，CD＝BC，AC与BD交于点E。

（1）求证：DC2＝CE·AC；

（2）若AE＝2EC，求之值；

（3）在（2）的条件下，过点C作⊙O的切线，交AB的延长线于点H，若S△ACH＝，求EC之长.

Answer 1

【答案】（1）证明见解析；（2）；（3）EC＝2

【解析】分析：(1)、根据题意得出△ACD和△DCE相似即可得出答案；(2)、设EC＝k，则AE＝2k，根据第一题的结论得出DC的长度，连接OC，OD，根据角平分线得出BD和DC的长度，根据Rt△ABC的性质得出AB的长度，从而得出∠BOD和∠DOA的度数，从而得出AD=AO，得出比值；(3)、设EC=k，根据切线的性质得出CG和AH的长度，最后根据△ACH的面积求出k的值．

详解：（1）证明：∵CD＝BC，∴∠DAC＝∠CDB，又∵∠ACD=∠DCE，∴△ACD∽△DCE，

∴，∴DC2＝CE·AC；

（2）设EC＝k，则AE＝2k，∴AC＝3k，由（1）DC2＝CE·AC＝3k2，

DC=k，连接OC，OD， ∵CD＝BC，∴OC平分∠DOB，∴BC＝DC＝k，

∵AB是⊙O的直径，∴在Rt△ACB中，，

∴OB=OC=OD=k，∴∠BOD＝120°，∴∠DOA＝60°，∴AD＝AO，∴ ；

（3）∵CH是⊙O的切线，连接CO，∴OC⊥CH．∵∠COH＝60°，∠H＝30°，

过C作CG⊥AB于G， 设EC=k，∵∠CAB＝30°，∴，

又∵∠H＝∠CAB＝30°，∴AC＝CH＝3k，∴AH＝，

∵S△ACH＝， ∴，∴k2＝4，k＝2，即EC＝2．