题目内容
【题目】以点A为顶点作两个等腰直角三角形(△ABC,△ADE),如图所示放置,使得一直角边重合,连接BD,CE.
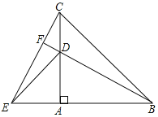
(1)求证:BD=CE;(2)延长BD,交CE于点F,求∠BFC的度数;
【答案】(1)详见解析;(2)90°.
【解析】
(1)根据等腰直角三角形的性质得到AB=AC,∠BAD=∠EAC=90°,AD=AE,利用“SAS”可证明△ADB≌△AEC,则BD=CE;
(2)由△ADB≌△AEC得到∠ACE=∠DBA,利用三角形内角和定理可得到∠BFC=180°-∠ACE-∠CDF=180°-∠DBA-∠BDA=∠DAB=90°;
(1)∵△ABC、△ADE是等腰直角三角形,
∴AB=AC,∠BAD=∠EAC=90°,AD=AE,
∵在△ADB和△AEC中,
 ,
,
∴△ADB≌△AEC(SAS),
∴BD=CE;
(2)∵△ADB≌△AEC,
∴∠ACE=∠ABD,
而在△CDF中,∠BFC=180°∠ACE∠CDF
又∵∠CDF=∠BDA
∴∠BFC=180°∠DBA∠BDA=∠DAB=90°;

【题目】2019年中国快递行业竞争激烈,为了占据市场赢得消费者青睐,某快递公司出台了市内快件收费标准:凡是重庆市内的快递统一收取基础费用8元,快递质量不超过10kg,不加收费用;快递质量大于10kg,则超过10g的部分按0.3元/kg收费.
(1)某同学需要将重量为x(x>10)千克的书籍在重庆市内同城快递回家,则该同学需付快递费用y元,用含x的代数式表示y.
(2)因国庆阅兵需要将一些纪念品从重庆寄往相距1800千米的北京,该快递公司获得这项任务后,调整了市外快件收费标准,收费标准如下表.已知纪念品重量为a千克,则纪念品从重庆运往北京的快递费为多少元?(用含a的代数式表示w)
价格表 | |
重量费 | 距离费 |
不超过10kg统一收取5元 | 0.01元/km |
超过10kg不超过50kg的部分0.2元/kg | |
超过50kg部分0.4元/kg | |
(注:快递费=重量费+距离费) | |
【题目】某商场,为了吸引顾客,在“白色情人节”当天举办了商品有奖酬宾活动,凡购物满200元者,有两种奖励方案供选择:一是直接获得20元的礼金券,二是得到一次摇奖的机会.已知在摇奖机内装有2个红球和2个白球,除颜色外其它都相同,摇奖者必须从摇奖机内一次连续摇出两个球,根据球的颜色(如表)决定送礼金券的多少.
球 | 两红 | 一红一白 | 两白 |
礼金券(元) | 18 | 24 | 18 |
(1)请你用列表法(或画树状图法)求一次连续摇出一红一白两球的概率.
(2)如果一名顾客当天在本店购物满200元,若只考虑获得最多的礼品券,请你帮助分析选择哪种方案较为实惠.




