题目内容
【题目】已知,如图坐标平面内,A(﹣2,0),B(0,﹣4),AB⊥AC,AB=AC,△ABC经过平移后,得△A′B′C′,B点的对应点B′(6,0),A,C对应点分别为A′,C′.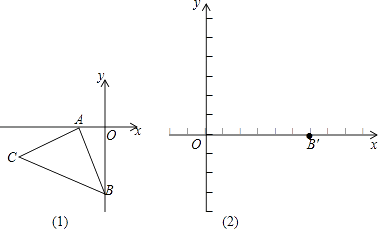
(1)求C点坐标;
(2)直接写出A′,C′坐标,并在图(2)中画出△A′B′C′;
(3)P为y轴负半轴一动点,以A′P为直角边以A’为直角顶点,在A′P右侧作等腰直角三角形A′PD.①试证明点D一定在x轴上;②若OP=3,求D点坐标.
【答案】
(1)
解:∵A(﹣2,0),B(0,﹣4),
∴AO=2,BO=4,
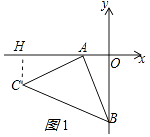
作CH⊥x轴于H,如图1所示:
则∠CHA=90°=∠AOB,
∴∠ACH+∠CAH=90°,
∵AB⊥AC,
∴∠BAO+∠CAH=90°,
∴∠ACH=∠BAO,
在△ACH和△BAO中, 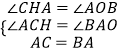 ,
,
∴△ACH≌△BAO(AAS),
∴AH=BO=4,CH=AO=2,
∴OH=AO+AH=6,
∴C(﹣6,﹣2)
(2)
解:∵B(0,﹣4),B′(6,0),
∴△ABC向上平移4个单位长度,再向右平移6个单位长度,
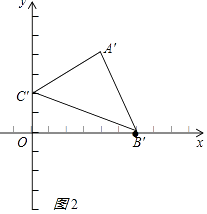
∴A′(4,4),C′(0,2)
(3)
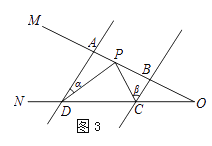
解:①连B′D,延长DB′交PC′于E,交A′P于F,如图3所示:
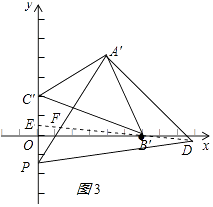
∵△A′B′C′和△A′PD是等腰直角三角形,
∴A′B′=A′C′,A′P=A′D,∠B′A′C′=∠DA′P=90°,
∴∠PA′C′=∠DA′B′,
在:△A′DB′和△A′PC′中, 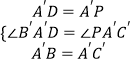 ,
,
∴△A′DB′≌△A′PC′(SAS),
∴∠A′DB′=∠A′PC′,
∵∠PFE=∠A′FD,
∴∠PEF=∠PA′D=90°,
∴DB′⊥y轴,
∴D点在x轴上;
②∵△A′DB′≌△A′PC′得,
∴B′D=C′P=5,
∴OD=11,
∴D(11,0).
【解析】(1)由点的坐标得出AO=2,BO=4,作CH⊥x轴于H,证出∠ACH=∠BAO,由AAS证明△ACH≌△BAO,得出AH=BO=4,CH=AO=2,求出OH=AO+AH=6,即可得出点C的坐标;C(﹣6,﹣2);(2)由B(0,﹣4)和B′(6,0),得出△ABC向上平移4个单位长度,再向右平移6个单位长度得△A′B′C′,即可得出A′,C′坐标,画出图形即可;(3)①连B′D,延长DB′交PC′于E,交A′P于F,由等腰直角三角形的性质得出A′B′=A′C′,A′P=A′D,∠B′A′C′=∠DA′P=90°,证出∠PA′C′=∠DA′B′,由SAS证明△A′DB′≌△A′PC′,得出∠A′DB′=∠A′PC′,由三角形内角和得出∠PEF=∠PA′D=90°,得出DB′⊥y轴,即可得出D点在x轴上;
②由全等三角形的性质得出B′D=C′P=5,得出OD=11,即可得出答案.