题目内容
【题目】问题情景:如图1,AB∥CD,∠PAB=140°,∠PCD=135°,求∠APC的度数.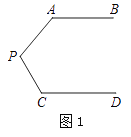
(1)丽丽同学看过图形后立即口答出:∠APC=85°,请你补全她的推理依据.
如图2,过点P作PE∥AB,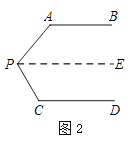
∵AB∥CD,∴PE∥CD. ()
∴∠A+∠APE=180°.
∠C+∠CPE=180°. ()
∵∠PAB=140°,∠PCD=135°,
∴∠APE=40°,∠CPE=45°
∴∠APC=∠APE+∠CPE=85°.()
问题迁移:
(2)如图3,AD∥BC,当点P在A、B两点之间运动时,∠ADP=∠α,∠BCP=∠β,求∠CPD与∠α、∠β之间有何数量关系?请说明理由.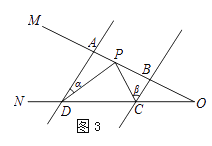
(3)在(2)的条件下,如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD与∠α、∠β之间的数量关系.
【答案】
(1)平行于同一条直线的两条直线平行,两直线平行,同旁内角互补,等量代换
(2)解:∠CPD=∠α+∠β,理由如下:
如图3所示,过P作PE∥AD交CD于E,
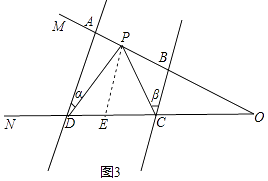
∵AD∥BC,
∴AD∥PE∥BC,
∴∠α=∠DPE,∠β=∠CPE,
∴∠CPD=∠DPE+∠CPE=∠α+∠β
(3)解:当P在BA延长线时,如图4所示:
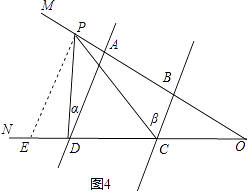
过P作PE∥AD交CD于E,
同(2)可知:∠α=∠DPE,∠β=∠CPE,
∴∠CPD=∠β﹣∠α;
当P在AB延长线时,如图5所示:
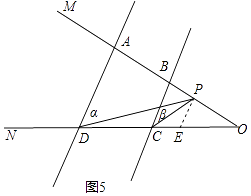
同(2)可知:∠α=∠DPE,∠β=∠CPE,
∴∠CPD=∠α﹣∠β.
【解析】(1)平行线间出现折线过点P作PE∥AB,
如图2所示:
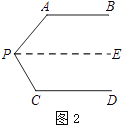
∵AB∥CD,
∴PE∥CD.(平行于同一条直线的两条直线平行)
∴∠A+∠APE=180°.
∠C+∠CPE=180°.(两直线平行同旁内角互补)
∵∠PAB=130°,∠PCD=120°,
∴∠APE=50°,∠CPE=60°
∴∠APC=∠APE+∠CPE=110°.(等量代换)
所以答案是:平行于同一条直线的两条直线平行|两直线平行,同旁内角互补|等量代换;
(2)类比第1题,过平行线间的折线折点,构造出内错角,转化∠α、∠β,可得结论;
(3)类比第1题,过平行线间的折线折点,构造出内错角,转化∠α、∠β,须分类讨论,可得结论.
【考点精析】本题主要考查了平行线的判定与性质的相关知识点,需要掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质才能正确解答此题.