题目内容
【题目】在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=30°,CD、BE交于点O,连接OA
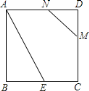
(1) 如图1,求证:△ABE≌△ACD
(2) 如图1,求∠AOE的大小
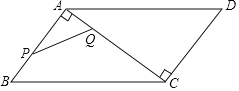
(3) 当绕点A旋转至如图2所示位置时,若∠BAC=∠DAE=α,∠AOE=_________

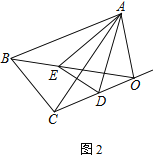
【答案】(1)见解析;(2)∠AOE=105°;(3)90°+![]() α.
α.
【解析】
(1)根据等边三角形的性质性质,可得∠BAE=∠CAD,由SAS证明△ABE≌△ACD即可;
(2)由等腰三角形的性质和三角形内角和定理得出∠ABC=∠ACB=75°,根据全等三角形的性质得出∠ABO=∠ACO.∠AEO=∠ADO,证出A、B、C、O四点共圆,A、D、E、O四点共圆,由圆内接四边形的性质和圆周角定理得出∠AOD=∠ABC=75°,∠DOE=∠DAE=30°,得出∠AOE=∠AOD+∠DOE=105°即可;
(3)同(2),即可得出结果.
(1)证明:∵∠BAC=∠DAE=30°,
∴∠BAC+∠CAE=∠DAE+∠CAE,
即∠BAE=∠CAD.
在△ABE和△ACD中,
 ,
,
∴△ABE≌△ACD(SAS);
(2)∵AB=AC,
∴∠ABC=∠ACB=![]() (180°30°)=75°,
(180°30°)=75°,
∵△ABE≌△ACD,
∴∠ABO=∠ACO.∠AEO=∠ADO,
∴A、B. C. O四点共圆,A. D. E. O四点共圆,
∴∠AOD=∠ABC=75°,∠DOE=∠DAE=30°,
∴∠AOE=∠AOD+∠DOE=75°+30°=105°;
(3)同(2)得:∠ABC=∠ACB=![]() (180°α)=90°
(180°α)=90°![]() α,
α,
∴∠AOD=∠ABC=90°![]() α,∠DOE=∠DAE=α,
α,∠DOE=∠DAE=α,
∴∠AOE=∠AOD+∠DOE=90°![]() α+α=90°+
α+α=90°+![]() α;
α;
故答案为:90°+![]() α.
α.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案