题目内容
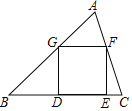
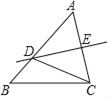
【题目】如图①，已知
是等腰三角形，
是
边上的高，垂足为
，
是底边
上的高，交于点
．
（1）若
．求证：
≌
；
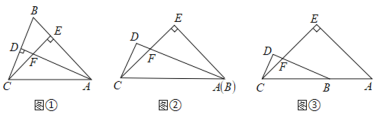
（2）在图②, 图③中，
是等腰直角三角形，点
在线段
上(不含点
)，
，且
交于点，
，垂足为
．
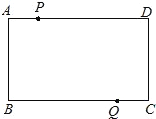
ⅰ）如图②，当点与点
重合，试写出
与的数量关系；
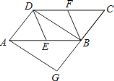
ⅱ）如图③，当点在线段上(不含点，)时，ⅰ）中的结论成立吗？如果成立，请证明；如果不成立，请说明理由．
【答案】（1）见解析；（2）ⅰ）
；ⅱ）成立，证明见解析
【解析】
（1）如图1，根据同角的余角相等证明
，利用ASA证明
≌
；
（2）①如图2，作辅助线，构建全等三角形，证明≌
，则CP=AF，再证明
≌
，可得结论；
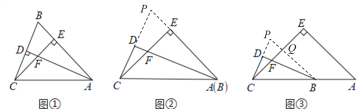
②结论仍然成立，过点
作
的平行线交
于
，且于
的延长线相交于点
，证明
≌
，得
，再证明
≌
即可求解．
证明：（1）∵
∴
∵
∴
在和中
∴≌；
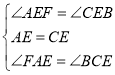
（2）ⅰ）：
证明过程如下：延长、交于点
∵
∴
∵
∴
∵
是等腰直角三角形，
∴AE=CE，
又
∴≌
∴
∵
∴
平分
则
∵
∴
又AD=AD
∴≌（ASA）
∴
∴
∴；
ⅱ）成立，即
证明如下：过点作的平行线交于，且于的延长线相交于点
∴
,
∴
=
∴
是等腰直角三角形，
∴CQ=QB
同理可得≌
∴
∵=
∴BD平分
则
∵
∴
=90
又BD=BD
∴≌（ASA）
∴
∴
∴．
练习册系列答案
孟建平名校考卷系列答案
相关题目
