Question

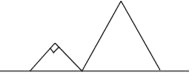
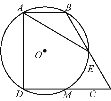
【题目】如图，直角梯形ABCD中，∠BAD=∠CDA=90°，AB=，CD=2，过A，B，D三点的☉O分别交BC，CD于点E，M，且CE=2，下列结论:①DM=CM；②弧AB=弧EM；③☉O的直径为2；④AE=.其中正确的结论是（ ）

A. ①②③ B. ①②④ C. ①③④ D. ①②③④

Answer 1

【答案】B

【解析】

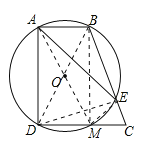
连接BD，BM，AM，EM，DE，利用三个角为直角的四边形为矩形得到ABMD为矩形，利用矩形的对边相等得到AB=DM，进而可证明DM=CM，故选项①正确；在Rt△DEC中，由M为CD的中点，利用斜边上的中线等于斜边的一半得到DM与EM相等，从而AB=EM，所以弧AB=弧EM，故选项②正确；先证明四边形AMCB为平行四边形，可得出AM=BC，等量代换得到BC=BD，由BD为圆的直径，可得△DEC为直角三角形，利用勾股定理可求出DE的长，设BE=x，则BD=BC=BE+EC=x+2，在Rt△BDE中，利用勾股定理列出关于x的方程，求出方程的解得到x的值，确定出BC的长，即为BD的长，确定出圆的直径，即可对于选项③作出判断；在Rt△AEM中，由AM与ME的长，利用勾股定理求出AE的长，即可对于选项④作出判断．

连接BD，BM，AM，EM，DE，

∵∠BAD=90°，

∴BD为圆的直径，

∴∠BMD=90°，

∴∠BAD=∠CDA=∠BMD=90°，

∴四边形ABMD矩形，

∴AB=DM，

又∵CD=2AB，

∴CD=2DM，即DM=MC；

故选项①正确；

在Rt△DEC中，M是DC中点，

∴EM=DM=CD=，

∴弧EM=弧DM，

又∵AB=DM，

∴弧AB=弧DM，

∴弧AB=弧EM，

故选项②正确；

∵AB∥MC，AB=MC，

∴四边形ABCM是平行四边形，

∴AM=BC，又BD=AM，

∴BD=BC，

∵BD是直径，

∴∠BED=90°，即∠DEC=90°，

又EC=2，DC=2，

根据勾股定理得：DE==2，

设BE=x，BD=BC=BE+EC=x+2，

在Rt△BDE中，根据勾股定理得：BE2+DE2=BD2，即x2+20=（x+2）2，

解得：x=4，

∴BD=6，故选项③错误；

在Rt△AEM中，AM=6，EM=，

根据勾股定理得：AE==；

故选项④正确；

则正确的选项为：①②④．

故选B.