题目内容
在△ABC中,P是BA延长线上一点,AE是∠CAP的平分线,CE⊥AE于E,BD⊥EA延长线于D.(1)若四边形BCED是正方形(如图①),AB、AC分别于CD、BE相交于点M、N,求证:△ADM≌△AEN.
(2)如图②,若AD=kAE,BE、CD相交于F.试探究EF、BF之间的数量关系,并说明理由.(用含k的式子表示)
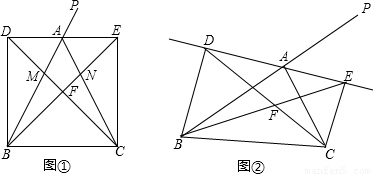
【答案】分析:(1)先根据对顶角相等得出∠DAB=∠PAE,再由AE平分∠PAC,∠DAB=∠EAC,根据四边形BCED是正方形,可知BD=CE,∠BDA=∠CEA=90°,由ASA定理得出△DAB≌△EAC(ASA),故可得出AD=AE,再由BE、CD是正方形BCDE的对角线可知∠MDA=∠NEA,由此即可得出结论;
(2)由(1)得∠DAB=∠EAC,再由相似三角形的判定定理得出△ABD∽△ACE,由AD=kAE可知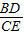 =
=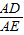 =k,根据BD∥CE,可得出∠FDB=∠FCE,∠FBD=∠FEC,故△DFB∽△CFE,根据相似三角形的性质可知
=k,根据BD∥CE,可得出∠FDB=∠FCE,∠FBD=∠FEC,故△DFB∽△CFE,根据相似三角形的性质可知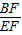 =
=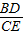 =k,由此即可得出结论.
=k,由此即可得出结论.
解答:(1)证明:∵∠DAB=∠PAE,AE平分∠PAC,
∴∠DAB=∠EAC,
又∵四边形BCED是正方形,
∴BD=CE,∠BDA=∠CEA=90°,
∴∠ABD=∠ACE,
在△DAB与△EAC中,
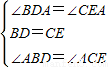 ,
,
∴△DAB≌△EAC(ASA),
∴AD=AE,
∵BE、CD是正方形BCDE的对角线,
∴∠MDA=∠NEA,
在△ADM与△AEN中,
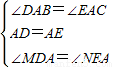 ,
,
∴△ADM≌△AEN(SAS);
(2)猜想:BF=kEF(或EF=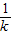 BF).
BF).
证明:由(1)得∠DAB=∠EAC,
∵∠BDA=∠CEA=90°,
∴△ABD∽△ACE,
∵AD=kAE,
∴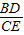 =
=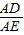 =k,
=k,
∵BD∥CE,
∴∠FDB=∠FCE,∠FBD=∠FEC,
∴△DFB∽△CFE,
∴ =
=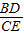 =k,
=k,
∴EF=kEF(或EF=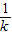 BF).
BF).
点评:本题考查的是相似形综合题,涉及到全等三角形及相似三角形的判定与性质,难度适中.
(2)由(1)得∠DAB=∠EAC,再由相似三角形的判定定理得出△ABD∽△ACE,由AD=kAE可知
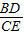 =
=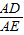 =k,根据BD∥CE,可得出∠FDB=∠FCE,∠FBD=∠FEC,故△DFB∽△CFE,根据相似三角形的性质可知
=k,根据BD∥CE,可得出∠FDB=∠FCE,∠FBD=∠FEC,故△DFB∽△CFE,根据相似三角形的性质可知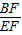 =
=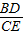 =k,由此即可得出结论.
=k,由此即可得出结论.解答:(1)证明:∵∠DAB=∠PAE,AE平分∠PAC,
∴∠DAB=∠EAC,
又∵四边形BCED是正方形,
∴BD=CE,∠BDA=∠CEA=90°,
∴∠ABD=∠ACE,
在△DAB与△EAC中,
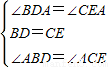 ,
,∴△DAB≌△EAC(ASA),
∴AD=AE,
∵BE、CD是正方形BCDE的对角线,
∴∠MDA=∠NEA,
在△ADM与△AEN中,
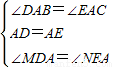 ,
,∴△ADM≌△AEN(SAS);
(2)猜想:BF=kEF(或EF=
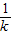 BF).
BF).证明:由(1)得∠DAB=∠EAC,
∵∠BDA=∠CEA=90°,
∴△ABD∽△ACE,
∵AD=kAE,
∴
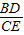 =
=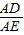 =k,
=k,∵BD∥CE,
∴∠FDB=∠FCE,∠FBD=∠FEC,
∴△DFB∽△CFE,
∴
 =
=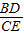 =k,
=k,∴EF=kEF(或EF=
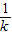 BF).
BF).点评:本题考查的是相似形综合题,涉及到全等三角形及相似三角形的判定与性质,难度适中.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
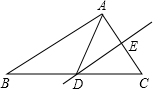 如图所示,在△ABC中,DE是AC的中垂线,AE=3cm,△ABD得周长为13cm,则△ABC的周长是
如图所示,在△ABC中,DE是AC的中垂线,AE=3cm,△ABD得周长为13cm,则△ABC的周长是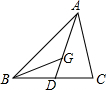 如图,在△ABC中,AD是中线,G是重心,
如图,在△ABC中,AD是中线,G是重心, 如图在△ABC中,AD是BC边上的高,BE平分∠ABD,交AD于E.已知∠BED=60°,∠BAC=50°,则∠C=( )
如图在△ABC中,AD是BC边上的高,BE平分∠ABD,交AD于E.已知∠BED=60°,∠BAC=50°,则∠C=( )