Question

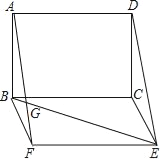
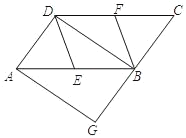
【题目】已知：如图，在ABCD中，AD＝4，AB＝8，E、F分别为边AB、CD的中点，BD是对角线，AG∥DB交CB的延长线于点G．

（1）求证：△ADE≌△CBF；

（2）若四边形BEDF是菱形，求四边形AGBD的面积．

Answer 1

【答案】（1）详见解析；（2）16

【解析】

（1）根据SAS证明△ADE≌△CBF即可．

（2）证明四边形ADBG是矩形，利用勾股定理求出BD即可解决问题．

（1）证明：∵四边形ABCD是平行四边形，

∴DA＝BC，∠DAE＝∠C，CD＝AB，

∵E、F分别为边AB、CD的中点，

∴AE＝AB，CF＝CD，

∴AE＝CF，

∴△ADE≌△CBF（SAS）．

（2）解：∵四边形ABCD是平行四边形，

∴AD∥BG，

∵BD∥AG，

∴四边形ADBG是平行四边形，

∵四边形BEDF是菱形，

∴DE＝BE，

∴AE＝EB，

∴DE＝AE＝EB，

∴∠ADE＝∠EAD，∠EDB＝∠EBD，

∵∠EAD+∠EDA+∠EDB+∠EBD＝180°，

∴∠EDA+∠EDB＝90°，

∴∠ADB＝90°，

∴四边形ADBG是矩形，

∵BD＝，

∴S矩形ADBG＝ADDB＝16．