题目内容
【题目】设一次函数y=kx+b(k,b是常数,k≠0)的图象过A(1,3),B(﹣1,﹣1)两点.
(1)求该一次函数的表达式;
(2)若点(2a+2,a2)在该一次函数图象上,求a的值.
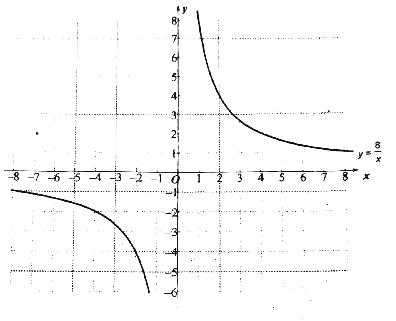
(3)已知点C(x1,y1)和点D(x2,y2)在该一次函数图象上,设m=(x1﹣x2)(y1﹣y2),判断反比例函数y=![]() 的图象所在的象限,说明理由.
的图象所在的象限,说明理由.
【答案】(1)y=2x+1;(2)a的值是﹣1或5;(3)在第一、三象限.
【解析】
(1)把A(1,3),B(-1,-1)两点坐标分别代入一次函数y=kx+b,进而求得k、b的值解答即可;
(2)将点(2a+2,a2)代入y=2x+1,进而求得a值即可;
(3)根据题意得![]() ,进而整理确定m+1的取值,结合反比例函数性质解答即可.
,进而整理确定m+1的取值,结合反比例函数性质解答即可.
(1)∵一次函数y=kx+b(k,b是常数,k≠0)的图象过A(1,3),B(﹣1,﹣1)两点,
∴![]() ,得
,得![]() ,
,
即该一次函数的表达式是y=2x+1;
(2)点(2a+2,a2)在该一次函数y=2x+1的图象上,
∴a2=2(2a+2)+1,
解得,a=﹣1或a=5,
即a的值是﹣1或5;
(3)反比例函数y=![]() 的图象在第一、三象限,
的图象在第一、三象限,
理由:根据题意得![]() ,
,
∴y1-y2=2(x1-x2),
∴m=(x1-x2)( y1-y2)=2(x1﹣x2)2,
∴m>0,则m+1>0,
∴反比例函数y=![]() 的图象在第一、三象限.
的图象在第一、三象限.
故答案为:(1)y=2x+1;(2)a的值是﹣1或5;(3)在第一、三象限.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目