题目内容
【题目】如图，已知矩形 OABC，O 为坐标原点，已知 A（4，0）、C（0，2），D 为边 OA 的中点，连接 BD，M 点与 C 点重合，N 为 x 轴上一点，MN∥BD， 直线 MN 沿着 x 轴向右平移．
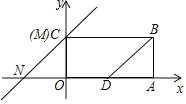
(1)当四边形 MBDN 为菱形时，N 点的坐标是 ；
(2)当 MN 平移到何处时，恰好将四边形 ODBC 的面积为 1：3 的两部分？请求出此时直线 MN 的解析式；
(3)在（1）的条件下，在矩形 OABC 的四条边上，是否存在点 F，连接 DF， 将矩形沿着 DF 所在的直线翻折，使得点 O 恰好落在直线 MN 上，若存在， 求出 F 点的坐标；若不存在，请说明理由．
【答案】（1）（2﹣2
，0）或（2+2，0）；（2）y＝x﹣
；（3） （0，2﹣2）或（2，2）．
【解析】
(1)由 MN∥BD，BM∥DN，推出四边形 MNDB 是平行四边形，当 DN
＝BD＝2时，四边形 MNDB 是菱形；(2)分两种情形构建方程即可解决问题；
(3)如图 1﹣1 中，过 D 作 GD⊥M1N1 交 M2N2 于 H，连接 OG、OH，作线段
OG 的垂直平分线交 OC 于 F，作线段 OH 的垂直平分线交 BC 于点 F′．点 F
与点 F′即为所
（1）如图 1 中，
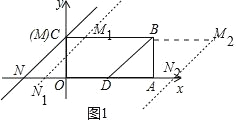
在 Rt△ABD 中，∵AD＝AB＝2，
∴BD＝ 
＝2，
∵MN∥BD，BM∥DN，
∴四边形 MNDB 是平行四边形，
当 DN＝BD＝2时，四边形 MNDB 是菱形，
∴N（2﹣2，0）或（2+2，0）．
故答案为（2﹣2，0）或（2+2，0）．
(2)如图 2 中，设 M（m，2）
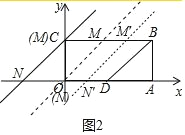
∵S 四边形 ODBC＝
×（2+4）×2＝6．
∴当直线 MN 经过点点 O 时，S△MCN＝×2×2＝2＝
S 四边形 ODBC，
∵将四边形 ODBC 的面积为 1：3 的两部分，
∴m＝
，
∴m＝
或﹣（舍弃），
此时直线 MN 的解析式为 y＝x+2﹣ ，
或满足：（4﹣m）2＝ ，解得 m＝
，
此时直线 MN 的解析式为 y＝x﹣．
(3)如图 1﹣1 中，过 D 作 GD⊥M1N1 交 M2N2 于 H，连接 OG、OH，作线段OG 的垂直平分线交 OC 于 F，作线段 OH 的垂直平分线交 BC 于点 F′．点 F 与点 F′即为所求．
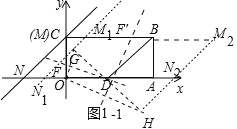
由题意可知 G（2﹣，），H（2+，﹣），
线段 OG 的垂直平分线的解析式为 y＝﹣（﹣1）x+2 ﹣2，可得 F（0，2﹣2），
线段 OH 的垂直平分线的解析式为 y＝（+1）x﹣2﹣2，可得 F′（2，2）．
