题目内容
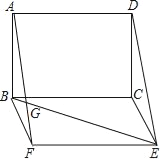
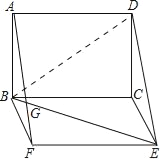
【题目】如图,已知矩形ABCD和BCEF,AF=BE,AF与BE交于点G,∠AGB=60°.
(1)求证:AF=DE;
(2)若AB=6,BC=8,求AF.
【答案】(1)证明见解析;(2)AF=10.
【解析】
(1)欲证明AF=DE,只要证明四边形ADEF是平行四边形即可;
(2)连接BD.利用勾股定理求出BD,再证明△BDE是等边三角形即可.
(1)∵四边形ABCD是矩形,
∴AD∥BC,AD=BC,
∵四边形BCEF是平行四边形,
∴BC∥EF,BC=EF,
∴AD=EF,AD∥EF,
∴四边形ADEF是平行四边形,
∴AF=DE;
(2)连接BD,
∵四边形ABCD是矩形,
∴∠BCD=90°,CD=AB=6,
∵BC=8,
∴BD=![]() =10,
=10,
∵四边形ADEF是平行四边形,
∴AF∥DE,
∴∠AGB=∠BED=60°,
∵AF=DE=BE,
∴△BDE是等边三角形,
∴AF=BE=BD=10.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目