题目内容
 (2012•南京二模)如图,在△ABC中,AB=AC,点O在∠BAC的平分线上,如果直线AB与⊙O相切,切点为B,试判断直线AC与⊙O的位置关系,并说明你的理由.
(2012•南京二模)如图,在△ABC中,AB=AC,点O在∠BAC的平分线上,如果直线AB与⊙O相切,切点为B,试判断直线AC与⊙O的位置关系,并说明你的理由.分析:直线AC与⊙O相切;根据切线AB的性质、角平分线的定义以及全等三角形的判定定理AAS证得△BAO≌△CAO;然后由全等三角形对应角相等知∠ACO=∠ABO=90°,即AC⊥OC;最后根据切线的定义证得AC是圆O的切线.
解答: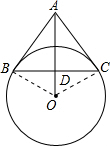 解:直线AC与⊙O相切;
解:直线AC与⊙O相切;
理由如下:连接OB、OC.
∵直线AB与⊙O相切,∴∠ABO=90°;
在△ABO和△ACO中,
∵点O在∠BAC的平分线上,
∴∠BAO=∠CAO.
又∵AB=AC,AO=AO.
∴△BAO≌△CAO,
∴OB=OC,∠ACO=∠ABO=90°,
∴AC⊥OC;
法一:∵直线AC过⊙O半径OC的外端点C,
∴直线AC与⊙O相切.
法二:∴圆心O到直线AC的距离是OC.
又∵OC=OB,
∴直线AC与⊙O相切.
 解:直线AC与⊙O相切;
解:直线AC与⊙O相切;理由如下:连接OB、OC.
∵直线AB与⊙O相切,∴∠ABO=90°;
在△ABO和△ACO中,
∵点O在∠BAC的平分线上,
∴∠BAO=∠CAO.
又∵AB=AC,AO=AO.
∴△BAO≌△CAO,
∴OB=OC,∠ACO=∠ABO=90°,
∴AC⊥OC;
法一:∵直线AC过⊙O半径OC的外端点C,
∴直线AC与⊙O相切.
法二:∴圆心O到直线AC的距离是OC.
又∵OC=OB,
∴直线AC与⊙O相切.
点评:本题考查了切线的判定与性质.注意,切点一定在圆上.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
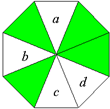 (2012•南京二模)如图所示的地面被分成8个全等的三角形区域,其中,标有字母a、b、c、d的4个三角形区域都是空地,另外4个三角形区域都是草坪.
(2012•南京二模)如图所示的地面被分成8个全等的三角形区域,其中,标有字母a、b、c、d的4个三角形区域都是空地,另外4个三角形区域都是草坪. (2012•南京二模)如图,把等腰直角三角形ABC沿直线BC方向向右平移到△DEF的位置,AC交DE于点O,连接AD,如果AB=2
(2012•南京二模)如图,把等腰直角三角形ABC沿直线BC方向向右平移到△DEF的位置,AC交DE于点O,连接AD,如果AB=2