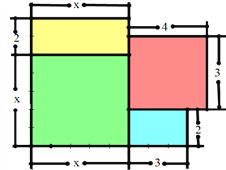
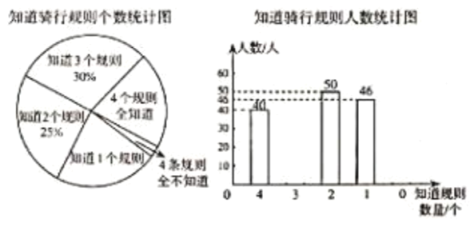
题目内容
【题目】如图,在平面直角坐标系中,一次函数y=-2x-4的图象与反比例函数![]() 的图象交于A(1,n),B(m,2).
的图象交于A(1,n),B(m,2).
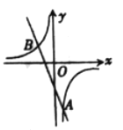
(1)求反比例函数关系式及m的值
(2)若x轴正半轴上有一点M,满足ΔMAB的面积为16,求点M的坐标;
(3)根据函数图象直接写出关于x的不等式![]() 的解集
的解集
【答案】(1) 反比例关系式为:![]() ,m=-3; (2)点M(2,0) ;(3)x<-3或0<x<1
,m=-3; (2)点M(2,0) ;(3)x<-3或0<x<1
【解析】
(1)把A(1,n),B(m,2)代入y=-2x-4即可求得m、n的值,从而得到A(1,-6),然后利用待定系数法即可即可求得反比例函数的表达式;
(2)设M(m,0),因为△MAB的面积为16,直线AB交x轴于(-2,0),可得![]() |m+2|×8=16,解方程即可;
|m+2|×8=16,解方程即可;
(3)根据图象,结合A、B的坐标即可求得.
解:(1) ∵一次函数y=-2x-4的图象过点A(1,n),B(m,2)
∴n=-2-4,2=-2m-4
∴n=-6,m=-3,
∴点A(1,-6).
把A(1,-6)代入![]() 得,k=-6,
得,k=-6,
∴反比例关系式为:![]() ;
;
(2)设直线AB交x轴于点N,则N(-2,0),设M(m,0),m>0,
当M在x轴正半轴时
![]()
![]()
=![]() |m+2|×8=16
|m+2|×8=16
∴m=2或-6(不合题意舍去),
∴点M(2,0) ;
(3) 由图象可知:不等式在![]() <-2x-4的解集是x<-3或0<x<1.
<-2x-4的解集是x<-3或0<x<1.
故答案为:(1) 反比例关系式为:![]() , m=-3; (2)点M(2,0) ;(3)x<-3或0<x<1
, m=-3; (2)点M(2,0) ;(3)x<-3或0<x<1

【题目】某校为了做好大课间活动,计划用400元购买10件体育用品,备选体育用品及单价如下表(单位:元)
备选体育用品 | 篮球 | 排球 | 羽毛球拍 |
单价(元) | 50 | 40 | 25 |
(1)若400元全部用来购买篮球和羽毛球拍共10件,问篮球和羽毛球拍各购买多少件?
(2)若400元全部用来购买篮球、排球和羽毛球拍三种共10件,能实现吗?(若能实现直接写出一种答案即可,若不能请说明理由.)