题目内容
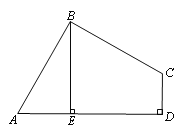
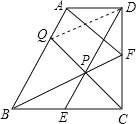
【题目】已知在直角梯形ABCD中, AD∥BC,∠BCD=90°, BC=CD=2AD , E、F分别是BC、CD边的中点,连结BF、DE交于点P,连结CP并延长交AB于点Q,连结AF,则下列结论不正确的是( )
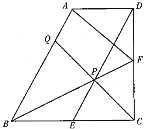
A.CP 平分∠BCDB.四边形 ABED 为平行四边形
C.CQ将直角梯形 ABCD 分为面积相等的两部分D.△ABF为等腰三角形
【答案】C
【解析】
A.根据边角边”证明△BCF≌△DCE,然后利用“角边角”证明△BEP≌△DFP,再利用“边角边”证明△BCP≌△DCP全等,根据全等三角形对应角相等可得∠BCP=∠DCP;
B.根据一组对边平行且相等的四边形是平行四边形可得四边形ABED为平行四边形;
C. 连接QD,利用“边角边”证明△BCQ和△DCQ全等,根据全等三角形的面积相等判断出S△BCQ=S△DCQ,判断出CQ将直角梯形ABCD分成的两部分面积不相等.
D. 根据平行四边形的对边相等可得AB=DE,再求出AB=BF,从而得到△ABF为等腰三角形;
解:∵BC=CD,E、F分别是BC、CD边的中点,
∴BE=CE=CF=DF,
在△BCF和△DCE中,
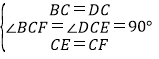 ,
,
∴△BCF≌△DCE(SAS),
∴DE=BF,∠CBF=∠CDE,∠BFC=∠DEC,
∴180°-∠BFC=180°-∠DEC,
即∠BEP=∠DFP,
在△BEP和△DFP中,
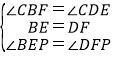 ,
,
∴△BEP≌△DFP(ASA),
∴BP=DP,
在△BCP和△DCP中,
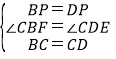 ,
,
∴△BCP≌△DCP(SAS),
∴∠BCP=∠DCP,
∴CP平分∠BCD,故A选项结论正确;
∵BC=2AD,E是BC的中点,
∴BE=AD,
又∵AD∥BC,
∴四边形ABED为平行四边形,故B选项结论正确;
∴AB=DE,
又∵DE=BF(已证),
∴AE=BF,
∴△ABF为等腰三角形,故D选项结论正确;
连接QD,
在△BCQ和△DCQ中,
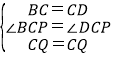 ,
,
∴△BCQ≌△DCQ(SAS),
∴S△BCQ=S△DCQ,
∴CQ将直角梯形ABCD分成的两部分面积不相等,故C选项结论不正确.
故选:C.

【题目】如图,是一张平行四边形纸片ABCD,要求利用所学知识作出一个菱形,甲、乙两位同学的作法分别如下:
甲:连接AC,作AC的中垂线交AD、BC于E、F,则四边形AFCE是菱形. | 乙:分别作 |
对于甲、乙两人的作法,可判断( )

A.甲正确,乙错误B.甲错误,乙正确
C.甲、乙均正确D.甲、乙均错误