题目内容
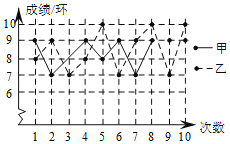
【题目】如图是甲、乙两射击运动员10次射击成绩的折线统计图，那么根据图中的信息估计，击中10环可能性更大的是__．
【答案】甲．
【解析】
根据所给的折线图求出甲、乙的平均成绩，再利用方差的公式进行计算，即可求出答案．
由图可知甲的成绩为9，7，8，9，8，9，7，9，9，9，
乙的成绩为8，9，7，8，10，7，9，10，7，10，
甲的平均数是：（9+7+8+9+8+9+7+9+9+9）÷10＝8.4，
乙的平均数是：（8+9+7+8+10+7+9+10+7+10）÷10＝8.5，
甲的方差S甲2＝[2×（7﹣8.4）2+2×（8﹣8.4）2+6×（9﹣8.4）2]÷10＝0.64，
乙的方差S乙2＝[3×（7﹣8.5）2+2×（8﹣8.5）2+2×（9﹣8.5）2+3×（10﹣8.5）2]÷10＝1.45，
则
，所以这10次射击成绩更稳定的运动员是甲．
故答案为：甲．
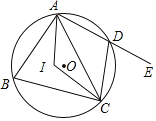
阅读快车系列答案
【题目】(本小题满分7分) 已知：如图，A是⊙O上一点，半径OC的延长线与过点A的直线交于B点，OC=BC，AC=
OB．
（1）求证：AB是⊙O的切线；
（2）若∠ACD=45°，OC=2，求弦CD的长．
【题目】如图为某商场的一个可以自由转动的转盘，规定：顾客购物满100元即可获得一次转动转盘的机会，当转盘停止时，指针落在哪一个区域就获得相应的奖品．下表是活动进行中的一组统计数据：
转动转盘的次数 | 100 | 150 | 200 | 500 | 800 | 1000 |
落在“钦料”的次数m | 71 | 110 | 155 | 379 | 603 | 752 |
根据以上信息，解决下列问题：
（1）请估计转动该转盘一次，获得饮料的概率约是 （精确到0.01）；
（2）现有若干个除颜色外相同的白球和黑球，根据（1）结论，在保证获得饮料与纸巾概率不变的情况下，请你设计一个可行的摸球抽奖规则，详细说明步骤；
（3）若小郑和小刘都购买超过100元的商品，均获得一次转动转盘的机会，请根据（2）中设计的规则，利用列表法或画树状图法求两人都获得“饮料”的概率．
