题目内容
 如图Rt△ABC中,∠ACB=90°,AC=4,AB=5,点P是AC上的一个动点(P不与点A、点C重合),PQ⊥AB,垂足为Q,当PQ与△ABC的内切圆⊙O相切时,PC的值为
如图Rt△ABC中,∠ACB=90°,AC=4,AB=5,点P是AC上的一个动点(P不与点A、点C重合),PQ⊥AB,垂足为Q,当PQ与△ABC的内切圆⊙O相切时,PC的值为
- A.

- B.1
- C.

- D.

C
分析:画出图形,证出△BCP′≌△BQ′P′,推出P′C=P′Q′,设P′C=P′Q′=a,证△AQ′P′∽△ACB,推出 =
= ,代入求出
,代入求出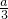 =
= ,求出a即可.
,求出a即可.
解答:
当PQ到P′Q′时,与⊙O相切,
此时OB平分∠CBA,OP′平分∠CP′Q′,且B、O、P′共线,
在△BCP′和△BQ′P′中
∵ ,
,
∴△BCP′≌△BQ′P′,
∴P′C=P′Q′,
设P′C=P′Q′=a,
∵∠A=∠A,∠C=∠P′Q′A=90°,
∴△AQ′P′∽△ACB,
∴ =
= ,
,
即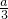 =
= ,
,
解得:a= ,
,
故选C.
点评:本题考查了相似三角形的性质和判定,全等三角形的性质和判定,三角形的内切圆等知识点,通过做此题培养了学生的推理能力,此题综合性比较强,有一定的难度.
分析:画出图形,证出△BCP′≌△BQ′P′,推出P′C=P′Q′,设P′C=P′Q′=a,证△AQ′P′∽△ACB,推出
 =
= ,代入求出
,代入求出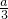 =
= ,求出a即可.
,求出a即可.解答:

当PQ到P′Q′时,与⊙O相切,
此时OB平分∠CBA,OP′平分∠CP′Q′,且B、O、P′共线,
在△BCP′和△BQ′P′中
∵
 ,
,∴△BCP′≌△BQ′P′,
∴P′C=P′Q′,
设P′C=P′Q′=a,
∵∠A=∠A,∠C=∠P′Q′A=90°,
∴△AQ′P′∽△ACB,
∴
 =
= ,
,即
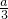 =
= ,
,解得:a=
 ,
,故选C.
点评:本题考查了相似三角形的性质和判定,全等三角形的性质和判定,三角形的内切圆等知识点,通过做此题培养了学生的推理能力,此题综合性比较强,有一定的难度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
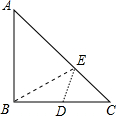 如图Rt△ABC中,AB=BC=4,D为BC的中点,在AC边上存在一点E,连接ED,EB,则△BDE周长的最小值为( )
如图Rt△ABC中,AB=BC=4,D为BC的中点,在AC边上存在一点E,连接ED,EB,则△BDE周长的最小值为( )A、2
| ||
B、2
| ||
C、2
| ||
D、2
|
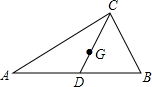 如图Rt△ABC中,∠C=90°,AC=8,BC=6,CD为AB边上的中线,点G是重心,则DG=
如图Rt△ABC中,∠C=90°,AC=8,BC=6,CD为AB边上的中线,点G是重心,则DG= 如图Rt△ABC中,∠C=90°,AC=12cm,BC=6cm,点P从B出发,以1cm/s的速度向C运动,同时点Q从C出发,以1cm/s的速度向A运动,问几秒时PQ的长为2
如图Rt△ABC中,∠C=90°,AC=12cm,BC=6cm,点P从B出发,以1cm/s的速度向C运动,同时点Q从C出发,以1cm/s的速度向A运动,问几秒时PQ的长为2
 已知:如图Rt△ABC中,∠C=Rt∠,AB=5,BC=4.
已知:如图Rt△ABC中,∠C=Rt∠,AB=5,BC=4.