题目内容
(2012•松北区三模)已知:如图Rt△ABC中,∠C=90°,CD是∠ACB的平分线,点M在线段AC上,点N在线段CD上.∠MND=∠ADN,NE∥BC,交BD于点E.
(1)(如图1)当点M和点A重合时,求证:AN=BE;
(2)(如图2)当MN:AD=2:3时,MC=NE,AM=2,延长MN交BC于点F,将线段BF以F为中心顺时针旋转,点B落在点P处,求出P点到BC的距离.
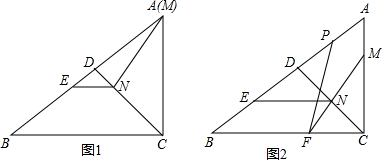
(1)(如图1)当点M和点A重合时,求证:AN=BE;
(2)(如图2)当MN:AD=2:3时,MC=NE,AM=2,延长MN交BC于点F,将线段BF以F为中心顺时针旋转,点B落在点P处,求出P点到BC的距离.

分析:(1)图1,作NH∥AB交BC于点H,由条件就可以得出四边形BHNE是平行四边形,再证明△ACN≌△HCN就可以得出结论;
(2)图2,作NH∥AB交BC于H,作MG∥AB交CD于G,作PQ⊥BC于Q,连接PM.可以得出四边形BHNE是平行四边形,就有HN=BE,再根据平行线的性质可以得出△CMG∽△CAD,由其性质可以得出CM的值,根据△MCN≌△END就有CN=DN,由中位线的性质可以得出BC的值,进一步证明△ABC∽△FMC就可以得出CF的值从而求出NF=PF,进而得出AP=AM,最后由平行线的性质就可以得出结论.
(2)图2,作NH∥AB交BC于H,作MG∥AB交CD于G,作PQ⊥BC于Q,连接PM.可以得出四边形BHNE是平行四边形,就有HN=BE,再根据平行线的性质可以得出△CMG∽△CAD,由其性质可以得出CM的值,根据△MCN≌△END就有CN=DN,由中位线的性质可以得出BC的值,进一步证明△ABC∽△FMC就可以得出CF的值从而求出NF=PF,进而得出AP=AM,最后由平行线的性质就可以得出结论.
解答:解:(1)作NH∥AB交BC于点H,
∵NE∥BC,
∴四边形BHNE是平行四边形,
∴BE=NH.
∵NH∥AB,
∴∠DNH=∠ADN.
∵∠MND=∠ADN,
∴∠DNH=∠ADN.
∵∠DNH+∠HNC=180°,
∠ADN+∠ANC=180°,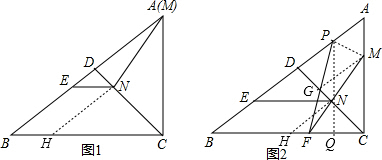
∴∠HNC=∠ANC.
∵CD是∠ACB的平分线,
∴∠HCN=∠ACN.
在△HNC和△ANC中,
,
∴△HNC≌△ANC(ASA),
∴HN=AN,
∴AN=BE;
(2)作NH∥AB交BC于H,作MG∥AB交CD于G,作PQ⊥BC于Q,连接PM.
∵EN∥BC,NH∥AB,
∴四边形BHNE是平行四边形,
∴HN=BE,
∵MG∥AB,
∴△CMG∽△CAD,∠MGN=∠ADN,
∴
=
.
∵∠MND=∠ADN,
∴∠MGN=∠MNG,
∴GM=NM.
∵MN:AD=2:3,
∴GM:AD=2:3.
∵AM=2,
∴AC=2+CM,
∴
=
,
∴CM=4.
∴AC=6.
∵EN∥BC,
∴∠END=∠BCD,∠DEN=∠B
∵∠MND=∠ADN,
∴∠MNC=∠EDN.
∵CD是∠ACB的平分线,
∴∠ACD=∠BCD.
∴∠ACD=∠END.
在△MCN和△END中,
,
∴△MCN≌△END(AAS)
∴CN=ND,∠CMN=∠NED.
∴N是CD的中点,∠CMN=∠B
∴BC=2EN.
∵MC=EN=4,
∴BC=8.
在△ABC和△FMC中,
,
∴△ABC∽△FMC,
∴
=
,
∴
=
,
∴FC=3.
∴BF=PF=5.
∴∠B=∠BPF,
∴∠BPF=∠FMC.
在Rt△MFC和Rt△ABC中,由勾股定理,得
MF=5.AB=10,
∴PF=MF,
∴∠FPM=∠FMP.
∴∠APM=∠AMP,
∴AP=AM=2.
∵PQ⊥BC,
∴∠PQB=90°,
∴∠ACB=90°,
∴∠PQB=∠ACB,
∴PQ∥AC,
∴
=
,
∴
=
,
∴PQ=4.8.
答:P点到BC的距离为4.8.
∵NE∥BC,
∴四边形BHNE是平行四边形,
∴BE=NH.
∵NH∥AB,
∴∠DNH=∠ADN.
∵∠MND=∠ADN,
∴∠DNH=∠ADN.
∵∠DNH+∠HNC=180°,
∠ADN+∠ANC=180°,

∴∠HNC=∠ANC.
∵CD是∠ACB的平分线,
∴∠HCN=∠ACN.
在△HNC和△ANC中,
|
∴△HNC≌△ANC(ASA),
∴HN=AN,
∴AN=BE;
(2)作NH∥AB交BC于H,作MG∥AB交CD于G,作PQ⊥BC于Q,连接PM.
∵EN∥BC,NH∥AB,
∴四边形BHNE是平行四边形,
∴HN=BE,
∵MG∥AB,
∴△CMG∽△CAD,∠MGN=∠ADN,
∴
| MG |
| AD |
| CM |
| AC |
∵∠MND=∠ADN,
∴∠MGN=∠MNG,
∴GM=NM.
∵MN:AD=2:3,
∴GM:AD=2:3.
∵AM=2,
∴AC=2+CM,
∴
| 2 |
| 3 |
| CM |
| 2+CM |
∴CM=4.
∴AC=6.
∵EN∥BC,
∴∠END=∠BCD,∠DEN=∠B
∵∠MND=∠ADN,
∴∠MNC=∠EDN.
∵CD是∠ACB的平分线,
∴∠ACD=∠BCD.
∴∠ACD=∠END.
在△MCN和△END中,
|
∴△MCN≌△END(AAS)
∴CN=ND,∠CMN=∠NED.
∴N是CD的中点,∠CMN=∠B
∴BC=2EN.
∵MC=EN=4,
∴BC=8.
在△ABC和△FMC中,
|
∴△ABC∽△FMC,
∴
| AC |
| BC |
| FC |
| MC |
∴
| 6 |
| 8 |
| FC |
| 4 |
∴FC=3.
∴BF=PF=5.
∴∠B=∠BPF,
∴∠BPF=∠FMC.
在Rt△MFC和Rt△ABC中,由勾股定理,得
MF=5.AB=10,
∴PF=MF,
∴∠FPM=∠FMP.
∴∠APM=∠AMP,
∴AP=AM=2.
∵PQ⊥BC,
∴∠PQB=90°,
∴∠ACB=90°,
∴∠PQB=∠ACB,
∴PQ∥AC,
∴
| PQ |
| AC |
| PB |
| AB |
∴
| PQ |
| 6 |
| 8 |
| 10 |
∴PQ=4.8.
答:P点到BC的距离为4.8.
点评:本题考查了全等三角形的判定与性质的运用,相似三角形的判定与性质的运用,勾股定理的运用,平行四边形的判定与性质的运用及三角形中位线的性质的运用,解答时正确作出辅助线是关键.

练习册系列答案
相关题目