题目内容
阅读理解,回答问题.
在解决数学问题的过程中,有时会遇到比较两数大小的问题,解决这类问题的关键是根据命题的题设和结论特征,采用相应办法,其中巧用“作差法”是解决此类问题的一种行之有效的方法:若a-b>0,则a>b;若a-b=0,则a=b;若a-b<0,则a<b.
例如:在比较m2+1与m2的大小时,小东同学的作法是:
∵(m2+1)-(m2)=m2+1-m2=1>0,
∴m2+1>m2.
请你参考小东同学的作法,解决如下问题:
(1)请你比较4 与(2+
与(2+ )2的大小;
)2的大小;
(2)已知a、b为实数,且ab=1,设M=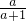 +
+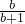 ,N=
,N=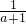 +
+ ,试比较M、N的大小;
,试比较M、N的大小;
(3)一天,小明爸爸的男同事来家做客,已知爸爸的年龄比小明年龄的平方大7岁,爸爸同事的年龄是小明年龄的5倍,请你帮忙算一算,小明该称呼爸爸的这位同事为“叔叔”还是“大伯”?
解:(1)∵ -(2+
-(2+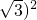 2
2
=4 -(4+4
-(4+4 +3)
+3)
=-7<0
∴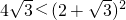
(2)∵M-N=(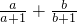 )-(
)-(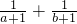 )
)
=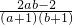
又∵ab=1
∴M-N=0
∴M=N
(3)设小明的年龄为x岁,则爸爸的年龄为(x2+7)岁,爸爸同事的年龄为5x岁.
∵(x2+7)-5x
=(x-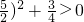 2+
2+
∴爸爸的年龄大,小明该称呼爸爸的这位同事为“叔叔”.
分析:(1)本题须通过计算4 与(2+
与(2+ )2的差即可得出结论.
)2的差即可得出结论.
(2)本题须通过计算M-N的值,即可比较出M、N的大小.
(3)本题需先设小明的年龄为x岁,再用x表示出爸爸的年龄和爸爸同事的年龄,最后求出爸爸的年龄和爸爸同事的年龄的差,即可得出谁的年龄大.
点评:本题主要考查了配方法的应用,在解题时要能根据题意列出式子并要配方法对列出的式子进行变形是本题的关键.
 -(2+
-(2+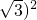 2
2=4
 -(4+4
-(4+4 +3)
+3)=-7<0
∴
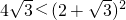
(2)∵M-N=(
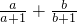 )-(
)-(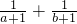 )
)=
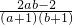
又∵ab=1
∴M-N=0
∴M=N
(3)设小明的年龄为x岁,则爸爸的年龄为(x2+7)岁,爸爸同事的年龄为5x岁.
∵(x2+7)-5x
=(x-
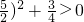 2+
2+
∴爸爸的年龄大,小明该称呼爸爸的这位同事为“叔叔”.
分析:(1)本题须通过计算4
 与(2+
与(2+ )2的差即可得出结论.
)2的差即可得出结论.(2)本题须通过计算M-N的值,即可比较出M、N的大小.
(3)本题需先设小明的年龄为x岁,再用x表示出爸爸的年龄和爸爸同事的年龄,最后求出爸爸的年龄和爸爸同事的年龄的差,即可得出谁的年龄大.
点评:本题主要考查了配方法的应用,在解题时要能根据题意列出式子并要配方法对列出的式子进行变形是本题的关键.

练习册系列答案
相关题目