题目内容
阅读理解并回答问题.
(1)观察下列各式:
=
=
-
,
=
=
-
,
=
=
-
,…
(2)找出规律,并计算:
+
+
+…+
+
(3)解方程:
+
+
+
+
=
.
(1)观察下列各式:
| 1 |
| 2 |
| 1 |
| 1×2 |
| 1 |
| 1 |
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 2×3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 12 |
| 1 |
| 3×4 |
| 1 |
| 3 |
| 1 |
| 4 |
(2)找出规律,并计算:
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 12 |
| 1 |
| (n-1)n |
| 1 |
| n(n+1) |
(3)解方程:
| 1 |
| (x-4)(x-3) |
| 1 |
| (x-3)(x-2) |
| 1 |
| (x-2)(x-1) |
| 1 |
| (x-1)x |
| 1 |
| x(x+1) |
| 1 |
| x+1 |
分析:(2)观察发现两个相邻正整数积的倒数等于它们的倒数的差;然后把式子
+
+
+…+
+
中得每个数转化为两个数的差,再进行加减运算即可;
(3)先根据(2)的规律变形为
-
+
-
+
-
+
-
+
-
=
,再整理可得
-
=
,然后去分母得x+1-(x+4)=x+4,解得x=-7,然后进行检验确定原方程的解.
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 12 |
| 1 |
| (n-1)n |
| 1 |
| n(n+1) |
(3)先根据(2)的规律变形为
| 1 |
| x |
| 1 |
| x+1 |
| 1 |
| x-1 |
| 1 |
| x |
| 1 |
| x-2 |
| 1 |
| x-1 |
| 1 |
| x-3 |
| 1 |
| x-2 |
| 1 |
| x-4 |
| 1 |
| x-3 |
| 1 |
| x+1 |
| 1 |
| x+4 |
| 1 |
| x+1 |
| 1 |
| x+1 |
解答:解:(2)规律为:
=
-
(n为正整数);
+
+
+…+
+
=1-
+
-
+
-
+…+
-
=1-
=
;
(3)
-
+
-
+
-
+
-
+
-
=
,
-
=
,
去分母得x+1-(x+4)=x+4,
解得x=-7,
经检验x=-7是原方程的解,
所以原方程的解为x=-7.
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 12 |
| 1 |
| (n-1)n |
| 1 |
| n(n+1) |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n+1 |
| n |
| n+1 |
(3)
| 1 |
| x |
| 1 |
| x+1 |
| 1 |
| x-1 |
| 1 |
| x |
| 1 |
| x-2 |
| 1 |
| x-1 |
| 1 |
| x-3 |
| 1 |
| x-2 |
| 1 |
| x-4 |
| 1 |
| x-3 |
| 1 |
| x+1 |
| 1 |
| x+4 |
| 1 |
| x+1 |
| 1 |
| x+1 |
去分母得x+1-(x+4)=x+4,
解得x=-7,
经检验x=-7是原方程的解,
所以原方程的解为x=-7.
点评:本题考查了解分式方程:先把分式方程化为整式方程,解整式方程,然后进行检验,把整式方程的解代入分式方程的分母中,若分母为零,则这个整式方程的解为分式方程的增根;若分母不为零,则这个整式方程的解为分式方程的解.

练习册系列答案
相关题目
 =
= =
= -
- =
= =
= ,
, =
= =
= ,
, =
=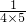 =
= ,
,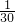 =
=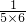 =
=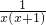 =______.
=______.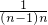 +
+
 +
+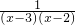 +
+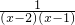 +
+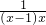 +
+