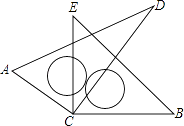��Ŀ����
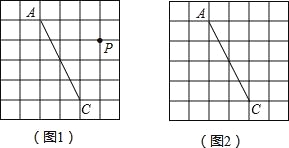
����Ŀ����ͼ����֪һ��ֱ��������ֽƬACB��������ACB=90�㣬AC=4��BC=3��E��F�ֱ���AC��AB���ϵ㣬����EF��
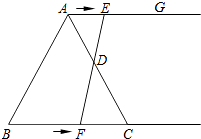
��1��ͼ�٣�����ֽƬACB��һ����EF�۵����۵����A����AB���ϵĵ�D������ʹS�ı���ECBF=3S��EDF����AE�ij���
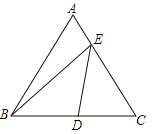
��2����ͼ�ڣ�����ֽƬACB��һ����EF�۵����۵����A����BC���ϵĵ�M������ʹMF��CA��
�����ж��ı���AEMF����״����֤����Ľ��ۣ�
����EF�ij���
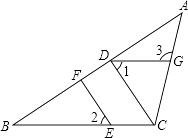
��3����ͼ�ۣ���FE���ӳ�����BC���ӳ��߽��ڵ�N��CN=1��CE=![]() ����
����![]() ��ֵ��
��ֵ��

���𰸡���1��![]() ����2�����ı���AEMFΪ���������������������
����2�����ı���AEMFΪ���������������������![]() ����3��
����3��![]() ��
��
��������
�����������1���������۵������ʵõ�EF��AB����AEF�ա�DEF����S��AEF��S��DEF������S��ABC=4S��AEF����֤��Rt��AEF��Rt��ABC��Ȼ��������������ε����ʵõ�![]() =��
=��![]() ��2�������ù��ɶ������AB���ɵõ�AE�ij�����2����ͨ��֤������������ж��ı���AEMFΪ���Σ�
��2�������ù��ɶ������AB���ɵõ�AE�ij�����2����ͨ��֤������������ж��ı���AEMFΪ���Σ�
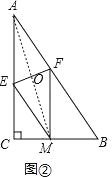
������AM��EF�ڵ�O����ͼ�ڣ���AE=x����EM=x��CE=4��x����֤����CME�ס�CBA�õ�![]() =
=![]() =
=![]() �����x������CM=
�����x������CM=![]() �������ù��ɶ��������AM��Ȼ��������ε������ʽ����EF��
�������ù��ɶ��������AM��Ȼ��������ε������ʽ����EF��
��3����ͼ�ۣ���FH��BC��H����֤����NCE�ס�NFH���������Ʊȵõ�FH��NH=4��7����FH=4x��NH=7x����CH=7x��1��BH=3����7x��1��=4��7x����֤����BFH�ס�BAC���������Ʊȿɼ����x=![]() ����ɼ����FH��BH���������ù��ɶ��������BF���Ӷ��õ�AF�ij������ǿɼ����
����ɼ����FH��BH���������ù��ɶ��������BF���Ӷ��õ�AF�ij������ǿɼ����![]() ��ֵ��
��ֵ��
�����������1����ͼ�٣�
�ߡ�ACB��һ����EF�۵����۵����A����AB���ϵĵ�D����
��EF��AB����AEF�ա�DEF��
��S��AEF��S��DEF��
��S�ı���ECBF=3S��EDF��
��S��ABC=4S��AEF��
��Rt��ABC�У��ߡ�ACB=90�㣬AC=4��BC=3��
��AB=![]() =5��
=5��
�ߡ�EAF=��BAC��
��Rt��AEF��Rt��ABC��
��![]() =��
=��![]() ��2������
��2������![]() ��2=
��2=![]() ��
��
��AE=![]() ��
��
��2�����ı���AEMFΪ���Σ��������£�
��ͼ�ڣ��ߡ�ACB��һ����EF�۵����۵����A����AB���ϵĵ�D����
��AE=EM��AF=MF����AFE=��MFE��
��MF��AC��
���AEF=��MFE��
���AEF=��AFE��
��AE=AF��
��AE=EM=MF=AF��
���ı���AEMFΪ���Σ�
������AM��EF�ڵ�O����ͼ�ڣ�
��AE=x����EM=x��CE=4��x��
���ı���AEMFΪ���Σ�
��EM��AB��
���CME�ס�CBA��
��![]() =
=![]() =
=![]() ����
����![]() =
=![]() =
=![]() �����x=
�����x=![]() ��CM=
��CM=![]() ��
��
��Rt��ACM��AM=![]() =
=![]() =
=![]() ��
��
��S����AEMF=![]() EFAM=AECM��
EFAM=AECM��
��EF=2��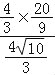 =
=![]() ��
��
��3����ͼ�ۣ���FH��BC��H��
��EC��FH��
���NCE�ס�NFH��
��CN��NH=CE��FH����1��NH=![]() ��FH��
��FH��
��FH��NH=4��7��
��FH=4x��NH=7x����CH=7x��1��BH=3����7x��1��=4��7x��
��FH��AC��
���BFH�ס�BAC��
��BH��BC=FH��AC������4��7x����3=4x��4�����x=![]() ��
��
��FH=4x=![]() ��BH=4��7x=
��BH=4��7x=![]() ��
��
��Rt��BFH��BF=![]() =2��
=2��
��AF=AB��BF=5��2=3��
��![]() =
=![]() ��
��


����Ŀ����ʦ��֪��ijУѧ��ÿ����ѧ·��Ҫ������ʱ�䣬�������ѡȡ30��ͬѧÿ����У�Ĵ���ʱ�䣨��λ�����ӣ�����ͳ�ƣ�ͳ�Ʊ����£�
ʱ�� | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 45 |
���� | 3 | 3 | 6 | 12 | 2 | 2 | 1 | 1 |
��1��д���������ݵ���λ����������
��2������30��ͬѧÿ����ѧ��ƽ��ʱ�䣮