题目内容
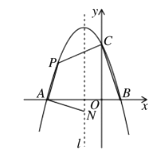
【题目】如图,已知AB是⊙O的直径,弦CD⊥AB于点E.点P是劣弧![]() 上任一点(不与点A,D重合),CP交AB于点M,AP与CD的延长相交于点F.
上任一点(不与点A,D重合),CP交AB于点M,AP与CD的延长相交于点F.

(1)设∠CPF=α,∠BDC=β,求证:α=β+90°;
(2)若OE=BE,设tan∠AFC=x,![]() .①求∠APC的度数;
.①求∠APC的度数;
②求y关于x的函数表达式及自变量x的取值范围.
【答案】(1)证明见解析;(2)①∠APC=60°;②y=![]() x,(0<x<
x,(0<x<![]() ).
).
【解析】
(1)CD⊥AB,则∠APC+∠CDB=90![]() ,即:180
,即:180![]() α+β=90
α+β=90![]() ,即可求解;
,即可求解;
(2)①证明△BOD为等边三角形,则∠CDB=30![]() ,即可求解;
,即可求解;
②在△CBM中,CH+HB=BC得:![]() ,
,![]() 得:
得:![]() ,即可求解.
,即可求解.
(1)∵CD⊥AB,
∴∠APC+∠CDB=90![]() ,即:180
,即:180![]() ﹣α+β=90
﹣α+β=90![]() ,
,
∴α=β+90![]() ;
;
(2)如图1,连接OD,
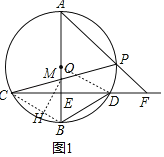
①OE=BE,OB⊥CD,设圆的半径为r,
∴∠BOD=∠OBD=∠ODB=60![]() ,
,
即:△BOD为等边三角形,
∴BC=r,
∴∠CDB=30![]() ,
,
∴∠APC=90![]() ﹣30
﹣30![]() =60
=60![]() ;
;
②连接BC,过点M组MH⊥BC于点H,
则∠MCB=∠FAB,∴∠CMH=∠F,
在△CBM中,设BC=r,∠CBA=60![]() ,
,
∴MH=BMsin∠CBA=![]() MB,
MB,
BH=![]() MB,CH=MHtan∠CMH=MHx,
MB,CH=MHtan∠CMH=MHx,
CH+HB=BC,即![]() ,
,
![]() ,而AM+BM=2r,
,而AM+BM=2r,
即:![]() ,
,
∴1![]() x=1+y,
x=1+y,
即:y=![]() x,(0<x
x,(0<x![]() ).
).

练习册系列答案
相关题目