题目内容
已知二次函数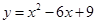
，当1≤x≤4,
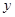的取值范围为 .
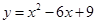，当1≤x≤4,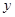的取值范围为 .
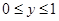.试题分析：先根据a=1判断出抛物线的开口向上，故有最小值，再把抛物线化为顶点式的形式可知对称轴x=3，最小值y=0，再根据1≤x≤4可知当x=4时y最大，把x=4代入即可得出结论．
试题解析：∵二次函数
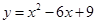中
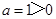，∴抛物线开口向上，有最小值，
∵
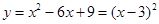，∴抛物线的对称轴
，∵
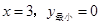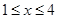，∴当x=4时，y最大=
．∴
．
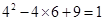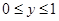练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
上的两点，则y1与y2的大小关系为y1 y2（填“>”“<”或“＝”）．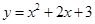
绕着它与y轴的交点旋转180°，所得抛物线的解析式为 ．
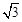,0)为圆心，以
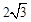为半径圆与x轴相交于点B，C，与y轴相交于点D，E.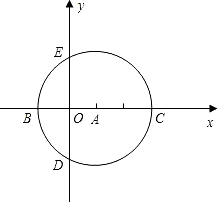
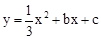经过点C，D两点，求抛物线的解析式，并判断点B是否在该抛物线上；
的顶点坐标是（ ）．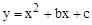
的图象上有两点(3，－8)和(－5，－8)，则此拋物线的对称轴是直线（ ）
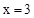
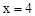
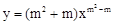是二次函数，则
＝________________________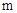