题目内容
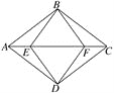
【题目】如图,ABCD是平行四边形,E、F是对角线AC上的两点,若∠ABF=∠CDE=90°.
(1)求证:四边形BEDF是平行四边形;
(2)若AB=AD=8,BF=6,求AE的长.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)由平行四边形的性质得出AB=CD,AB∥CD,证出∠BAC=∠DCA,由ASA证明△ABF≌△CDE,得出BF=DE,∠AFB=∠CED,证出BF∥DE,即可得出结论;
(2)连接BD交AC于G,证明四边形ABCD是菱形,得出AC⊥BD,证出四边形BEDF是菱形,得出BE=BF=6,由勾股定理求出AF,由三角形的面积关系求出BG,再由勾股定理求出EG,即可得出结果.
(1)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠BAC=∠DCA,
在△ABF和△CDE中,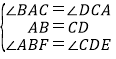 ,
,
∴△ABF≌△CDE(ASA),
∴BF=DE,∠AFB=∠CED,
∴BF∥DE,
∴四边形BEDF是平行四边形;
(2)连接BD交AC于G,如图所示:
∵AB=AD,
∴四边形ABCD是菱形,
∴AC⊥BD,
∴四边形BEDF是菱形,
∴BE=BF=6,EG=FG,
∵∠ABF=90°,AB=AD=8,BF=6,
∴AF=![]() =10,
=10,
∵△ABF的面积=![]() AF·BG=
AF·BG=![]() AB×BF,
AB×BF,
∴BG=![]() =
=![]() ,
,
∴EG=![]() =
=![]() ,
,
∴AE=AF-2EG=10-2×![]() =
=![]() .
.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目