Question

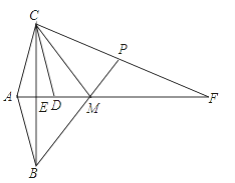
【题目】如图，平面直角坐标系中，已知点且为轴上点右侧的动点，以为腰作等腰，使直线交轴于点．

（1）求证：；

（2）求证：；

（3）当点运动时，点在轴上的位置是否发生改变，为什么？

Answer 1

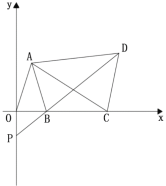
【答案】（1）见解析（2）见解析（3）点P在y轴上的位置不发生改变，理由见解析

【解析】

（1）根据算术平方根和平方数的非负性质即可求得a、b的值，即可求得A，B点坐标，即可求得OA，AB长度，即可解题；

（2）易证∠OAC＝∠BAD，即可证明△OAC≌△BAD，可得OC＝BD，即可解题；

（3）点P在y轴上的位置不发生改变．理由：设∠AOB＝∠ABO＝，易证∠OBP是定值，根据OB长度固定和∠POB＝90，即可解题．

（1）∵，

≥0，≥0，

∴a＋b3＝0，a2b＝0，

解得：a＝2，b＝1，

∴A（1，3），B（2，0），

∴OA＝，

AB＝，

∴OA＝AB；

（2）∵∠CAD＝∠OAB，

∴∠CAD＋∠BAC＝∠OAB＋∠BAC，即∠OAC＝∠BAD，

在△OAC和△BAD中，

，

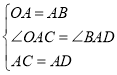∴△OAC≌△BAD（SAS），

∴OC＝BD；

（3）点P在y轴上的位置不发生改变．

理由：设∠AOB＝∠ABO＝，

∵由（2）知△AOC≌△ABD，

∴∠ABD＝∠AOB＝，

∵OB＝2，∠OBP＝180°∠ABO∠ABD＝180°2α为定值，

∵∠POB＝90，

∴OP长度不变，

∴点P在y轴上的位置不发生改变．