Question

【题目】在△ABC中，AB=BC，△ABC≌△A1BC1，A1B交AC于点E，A1C1分别交AC、BC于D、F两点，观察并猜想线段EA1与FC有怎样的数量关系？并证明你的结论．

Answer 1

【答案】EA1=FC．理由见解析.

【解析】

根据已知条件利用ASA证明△ABE≌△C1BF，然后根据全等三角形的性质以及线段的和差即可得到EA1=FC.

EA1=FC，理由如下：

∵AB=BC，

∴∠A=∠C，

∵△ABC≌△A1BC1

∴∠A=∠A1=∠C=∠C1

∴AB=A1B=BC=BC1，

∠ABC=∠A1B C1，

∴∠ABC﹣∠A1B C=∠A1B C1﹣∠A1B C，

∴∠ABE=∠C1BF，

在△ABE与△C1BF中，

，

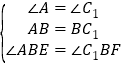∴△ABE≌△C1BF，

∴BE=BF，

∴A1B﹣BE=BC﹣BF，

∴EA1=FC.