题目内容
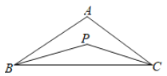
【题目】在△ABC中,已知∠ABC=60°,∠ACB=50°,BE是AC上的高,CF是AB上的高,H是BE和CF的交点.求∠ABE、∠ACF和∠BHC的度数.
【答案】∠ABE=20°;∠ACF=20°;∠BHC=110°.
【解析】
先利用三角形内角和求得∠A的度数,则在直角△ABE和直角△ACF中利用三角形内角和即可求得∠ABE和∠ACF的度数;再根据角的和差关系求出∠EBC和∠BCH的度数,然后在△BCH中利用三角形内角和即可求出∠BHC的度数.
解:∵BE是AC上的高,∴∠AEB=90°.
∵∠ABC=60°,∠ACB=50°,
∴∠A=180°﹣60°﹣50°=70°,
∴∠ABE=180°﹣90°﹣70°=20°.
∵CF是AB上的高,∴∠AFC=90°,
∴∠ACF=180°﹣90°﹣70°=20°.
∵∠ABE=20°,∴∠EBC=∠ABC﹣∠ABE=60°﹣20°=40°.
∵∠ACF=20°,∠ACB=50°,∴∠BCH=30°,
∴∠BHC=180°﹣40°﹣30°=110°.

练习册系列答案
相关题目