题目内容
【题目】综合与探究:
在平面直角坐标系中,已知点![]() ,点
,点![]() 是
是![]() 轴上的一个动点.
轴上的一个动点.

自主探究:
(1)点![]() 到
到![]() 轴的距离是_______,到原点的距离是 .
轴的距离是_______,到原点的距离是 .
(2)点![]() 关于
关于![]() 轴的对称点坐标为________,关于原点的对称点的坐标为 .
轴的对称点坐标为________,关于原点的对称点的坐标为 .
探索发现:
(3)当![]() 取何值时,
取何值时,![]() 是等腰三角形?
是等腰三角形?
【答案】(1)1,![]() ;(2)
;(2)![]() ,
,![]() ;(3)
;(3)![]() 的值为
的值为![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
(1)根据坐标与图形性质得到点P到x轴的距离,根据勾股定理求出点P到原点的距离;
(2)根据坐标关于y轴以及原点对称的特点即可得出点P的对称点的坐标;
(3)因为![]() ,当
,当![]() ,
,![]() ,
,![]() 时,分三种情况分别讨论即可求得答案.
时,分三种情况分别讨论即可求得答案.
(1)点P的坐标为(-2,-1),
点P到x轴的距离为:![]() ,
,
到原点的距离为:![]() ,
,
故答案为:1,![]() ;
;
(2)关于y轴对称,纵坐标不变,横坐标为相反数,
∴点P(-2,-1)关于y轴的对称点的坐标为(2,-1),
关于原点对称,横、纵坐标都为其相反数,
∴点P关于原点的对称点的坐标为(2,1),
故答案为:(2,-1),(2,1);
(3)∵![]() ,
,
①当![]() 时,
时,![]() 为等腰三角形,
为等腰三角形,![]() ,
,
若动点![]() 在原点左侧,则有
在原点左侧,则有![]() ;
;
若动点![]() 在原点右侧,则有
在原点右侧,则有![]() ;
;
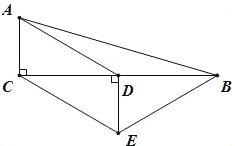
②如图1,当![]() 时,
时, ![]() 为等腰三角形,过点
为等腰三角形,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,
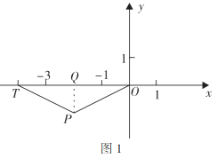
则点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,则有
对称,则有![]() ;
;
③如图2,当![]() 时,
时,![]() 为等腰三角形,过点
为等腰三角形,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,
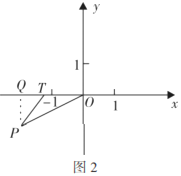
则![]() ,
,
在![]() 中,
中,![]() ,即
,即![]() ,
,
解得:![]() ,
,
∴ ![]() .
.
综上所述,当![]() 的值取
的值取![]() 或
或![]() 或
或![]() 或
或![]() 时,
时,![]() 为等腰三角形.
为等腰三角形.

【题目】某校组织全校2000名学生进行了环保知识竞赛,为了解成绩的分布情况,随机抽取了部分学生的成绩(得分取整数,满分为100分),并绘制了频数分布表和频数分布直方图(不完整):
分组 | 频数 | 频率 |
50.5~60.5 | 20 | 0.05 |
60.5~70.5 | 48 | △ |
70.5~80.5 | △ | 0.20 |
80.5~90.5 | 104 | 0.26 |
90.5~100.5 | 148 | △ |
合计 | △ | 1 |
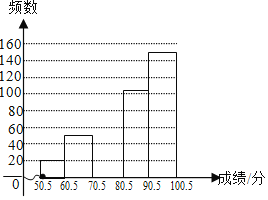
根据所给信息,回答下列问题 :
(1)补全频数分布表;
(2)补全频数分布直方图;
(3)学校将对成绩在 90.5 ~ 100.5 分之间的学生进行奖励,请你估算出全校获奖学生的人数 .