题目内容
【题目】如图,AB是⊙O的直径,点C,D是半圆O的三等分点,过点C作⊙O的切线交AD的延长线于点E,过点D作DF⊥AB于点F,交⊙O于点H,连接DC,AC. 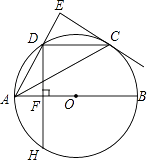
(1)求证:∠AEC=90°;
(2)试判断以点A,O,C,D为顶点的四边形的形状,并说明理由;
(3)若DC=2,求DH的长.
【答案】
(1)证明:连接OC,

∵EC与⊙O切点C,
∴OC⊥EC,
∴∠OCE=90°,
∵点CD是半圆O的三等分点,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴∠DAC=∠CAB,
∵OA=OC,
∴∠CAB=∠OCA,
∴∠DAC=∠OCA,
∴AE∥OC(内错角相等,两直线平行)
∴∠AEC+∠OCE=180°,
∴∠AEC=90°
(2)解:四边形AOCD为菱形.
理由是:
∵ ![]() =
= ![]() ,
,
∴∠DCA=∠CAB,
∴CD∥OA,
又∵AE∥OC,
∴四边形AOCD是平行四边形,
∵OA=OC,
∴平行四边形AOCD是菱形(一组邻边相等的平行四边形是菱形)
(3)解:连接OD.

∵四边形AOCD为菱形,
∴OA=AD=DC=2,
∵OA=OD,
∴OA=OD=AD=2,
∴△OAD是等边三角形,
∴∠AOD=60°,
∵DH⊥AB于点F,AB为直径,
∴DH=2DF,
在Rt△OFD中,sin∠AOD= ![]() ,
,
∴DF=ODsin∠AOD=2sin60°= ![]() ,
,
∴DH=2DF=2 ![]() .
.
【解析】(1)连接OC,根据EC与⊙O切点C,则∠OCE=90°,由题意得 ![]() =
= ![]() =
= ![]() ,∠DAC=∠CAB,即可证明AE∥OC,则∠AEC+∠OCE=180°,从而得出∠AEC=90°;(2)四边形AOCD为菱形.由(1)得
,∠DAC=∠CAB,即可证明AE∥OC,则∠AEC+∠OCE=180°,从而得出∠AEC=90°;(2)四边形AOCD为菱形.由(1)得 ![]() =
= ![]() ,则∠DCA=∠CAB可证明四边形AOCD是平行四边形,再由OA=OC,即可证明平行四边形AOCD是菱形(一组邻边相等的平行四边形是菱形);(3)连接OD.根据四边形AOCD为菱形,得△OAD是等边三角形,则∠AOD=60°,再由DH⊥AB于点F,AB为直径,在Rt△OFD中,根据sin∠AOD=
,则∠DCA=∠CAB可证明四边形AOCD是平行四边形,再由OA=OC,即可证明平行四边形AOCD是菱形(一组邻边相等的平行四边形是菱形);(3)连接OD.根据四边形AOCD为菱形,得△OAD是等边三角形,则∠AOD=60°,再由DH⊥AB于点F,AB为直径,在Rt△OFD中,根据sin∠AOD= ![]() ,求得DH的长.
,求得DH的长.
【考点精析】认真审题,首先需要了解切线的性质定理(切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径),还要掌握解直角三角形(解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法))的相关知识才是答题的关键.

 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案