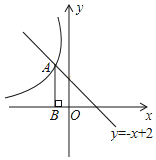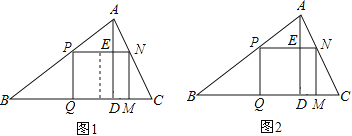题目内容
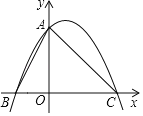
【题目】如图,抛物线![]() 过
过![]() ,
,![]() 两点.
两点.
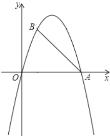
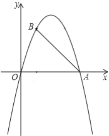
备用图
(1)求该抛物线的解析式;
(2)点P是抛物线上一点,且位于第一象限,当![]() 的面积为3时,求出点P的坐标;
的面积为3时,求出点P的坐标;
(3)过B作![]() 于C,连接OB,点G是抛物线上一点,当
于C,连接OB,点G是抛物线上一点,当![]() 时,请直接写出此时点G的坐标.
时,请直接写出此时点G的坐标.
【答案】(1)抛物线表达式为:![]() ;(2)点P坐标为
;(2)点P坐标为![]() ,
,![]() ,
,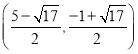 (3)点G坐标为
(3)点G坐标为![]() ,
,![]() .
.
【解析】
(1)利用待定系数法求抛物线表达式.
(2)设P点横坐标为m,当1<m<4时,过点P作PM∥y轴,交AB于点M,连接BP、AP,通过三角形的面积先求出PM的长,然后利用m表示PM的长,即可求出m,从而得到P点坐标;当0<m<1时,如图,过点P作PN∥x轴,交AB于点N,连接BP、AP,先通过三角形面积求出PN的长,可用m表示N点的横坐标,令P和N的纵坐标相等即可求出m,从而求出P点的坐标.综上即可得到答案.
(3)通过已知条件,得到∠BAO为45°,然后分点G在AB上方和下方两种情况讨论即可.
解:(1)把点A(4,0),B(1,3)代入抛物线y=ax2+bx
得![]()
解得![]()
∴抛物线表达式为:y=-x2+4x;
(2)设P点横坐标为m,
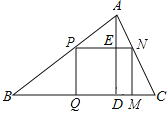
当1<m<4时,如图,过点P作PM∥y轴,交AB于点M,连接BP、AP,
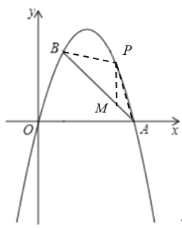
由于A(4,0),B(1,3)
∴![]() ,
,
∴PM=2,
设直线AB的解析式为y=kx+b,
将A(4,0),B(1,3)代入y=kx+b,
![]() ,
,
解得![]() ,
,
∴直线AB的解析式为y=-x+4,
设![]() ,
,![]() ,
,
则PM=![]() ,
,
∴![]() ,
,
解得,m=2或m=3,
∴P点坐标为![]() 或
或![]()
当0<m<1时,如图,过点P作PN∥x轴,交AB于点N,连接BP、AP,
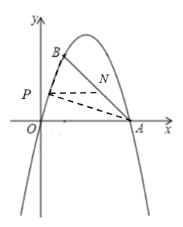
∴![]() ,
,
∴PN=2,
设![]() ,
,
则N点横坐标为m+2,∴![]() ,
,
由于PN两点纵坐标相同,
∴![]() ,
,
解得,![]() (舍去),
(舍去),![]()
∴P点坐标为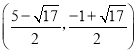 ,
,
综上所述,点P坐标为![]() ,
,![]() ,
,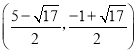 .
.
(3)如下图,过点A作AE⊥x轴,过点G作GE⊥y轴,交AE于点E,
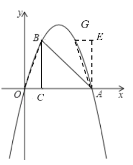
易得∠BAC=45°,
若![]() ,
,
则∠OBC=∠GAE,
∴△BOC∽△AGE,即AE=3GE,
设![]() ,则
,则![]()
解得,n=3或n=4(舍去)
∴G![]() ,
,
如下图,连接AG交BC于点F,
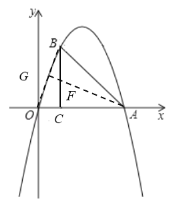
若![]() ,
,
则∠OBC=∠GAO,
易得,△OBC≌△FAC,
∴F(1,1)
可得直线AF的解析式为![]()
联立解析式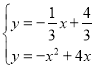
解得,x=4(舍去)或x=![]() ,
,
∴G![]() ,
,
综上所述,G![]() ,G
,G![]() .
.