题目内容
(2009•同安区质检)(1)计算:
+(-2009)0-(
)-1+4sin30°.
(2)先化简,再求值:a(a+2)-a2,其中a=-
.
(3)解方程:
=
.
| 4 |
| 1 |
| 3 |
(2)先化简,再求值:a(a+2)-a2,其中a=-
| 1 |
| 2 |
(3)解方程:
| 2 |
| x-3 |
| 3 |
| x-2 |
分析:(1)本题涉及二次根式、零指数幂、负整数指数幂、特殊角的三角函数值四个考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果;
(2)先去括号,再合并同类项将多项式化简,然后将a=-
代入,计算即可;
(3)观察可得最简公分母是(x-3)(x-2),方程两边乘最简公分母,可以把分式方程转化为整式方程求解.
(2)先去括号,再合并同类项将多项式化简,然后将a=-
| 1 |
| 2 |
(3)观察可得最简公分母是(x-3)(x-2),方程两边乘最简公分母,可以把分式方程转化为整式方程求解.
解答:解:(1)原式=2+1-3+4×
=2;
(2)原式=a2+2a-a2=2a,
当a=-
时,原式=-1;
(3)去分母,得 2(x-2)=3(x-3),
解这个方程,得 x=5.
检验:当x=5时,(x-3)(x-2)=6≠0,
故x=5是原方程的解.
| 1 |
| 2 |
(2)原式=a2+2a-a2=2a,
当a=-
| 1 |
| 2 |
(3)去分母,得 2(x-2)=3(x-3),
解这个方程,得 x=5.
检验:当x=5时,(x-3)(x-2)=6≠0,
故x=5是原方程的解.
点评:本题考查了实数与整式的综合运算及分式方程的解法,它们是各地中考题中常见的计算题型.进行实数的运算时,要熟记特殊角的三角函数值,掌握负整数指数幂、零指数幂、二次根式等考点的运算;解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解;解分式方程一定注意要验根.

练习册系列答案
相关题目
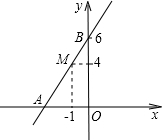 (2009•同安区质检)如图,一次函数的图象经过M点,与x轴交于A点,与y轴交于B点,根据图中信息求:
(2009•同安区质检)如图,一次函数的图象经过M点,与x轴交于A点,与y轴交于B点,根据图中信息求: