题目内容
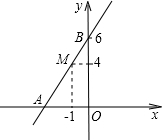 (2009•同安区质检)如图,一次函数的图象经过M点,与x轴交于A点,与y轴交于B点,根据图中信息求:
(2009•同安区质检)如图,一次函数的图象经过M点,与x轴交于A点,与y轴交于B点,根据图中信息求:(1)直线AB的函数关系式;
(2)若点P(m,n)是直线AB上的一动点,且-3≤m≤2,求n的取值范围.
分析:(1)首先设直线AB的关系式是y=kx+b(k≠0)然后把B(0,6),M(-1,4)代入函数解析式,可得到一个关于k、b的方程组,再解方程组即可求出函数关系式;
(2)根据函数解析式y=-2x+4,把P(m,n)代入可得n=-2m+4,再根据一次函数的性质可知n随着m的增大而减小,再根据m的取值范围确定n的取值范围.
(2)根据函数解析式y=-2x+4,把P(m,n)代入可得n=-2m+4,再根据一次函数的性质可知n随着m的增大而减小,再根据m的取值范围确定n的取值范围.
解答:解:(1)设直线AB的关系式是y=kx+b(k≠0),
∵图象经过B(0,6),M(-1,4),
∴
,
解得
,
故y=2x+6;
(2)∵点P(m,n)是直线AB上的一动点,
∴n=2m+6,
∵2>0,
∴n随着m的增大而增大,
∴当m取最小值时,n最小,
∵-3≤m≤2,
∴当m=-3时,n的最小值=0.
当m=2时,n的最大值=10,
∴0≤n≤10.
∵图象经过B(0,6),M(-1,4),
∴
|
解得
|
故y=2x+6;
(2)∵点P(m,n)是直线AB上的一动点,
∴n=2m+6,
∵2>0,
∴n随着m的增大而增大,
∴当m取最小值时,n最小,
∵-3≤m≤2,
∴当m=-3时,n的最小值=0.
当m=2时,n的最大值=10,
∴0≤n≤10.
点评:此题主要考查了待定系数法求一次函数关系式,以及一次函数的性质,一次函数的性质:k>0,y随x的增大而增大,函数从左到右上升;k<0,y随x的增大而减小,函数从左到右下降.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
