题目内容
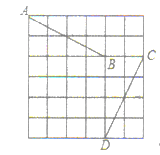
【题目】如图,在△ABC中AB=AC,△AED中AE=AD,∠EAD=∠BAC,AC与BD交于点O.
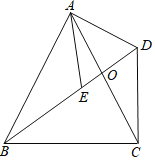
(1)试确定∠ADC与∠AEB间的数量关系,并说明理由;
(2)若∠ACB=65°,求∠BDC的度数.
【答案】(1)∠ADC=∠AEB,理由见解析;(2)50°
【解析】
(1)根据全等三角形的判定和性质证明即可;
(2)利用三角形的外角性质和三角形的内角和解答即可.
解:(1)∠ADC=∠AEB,理由如下:
∵∠BAC=∠EAD
∴∠BAC﹣∠EAC=∠EAD﹣∠EAC
即:∠BAE=∠CAD
在△ABE和△ACD中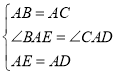
∴△ABE≌△ACD(SAS)
∴∠ADC=∠AEB
(2)∵∠BOC是△ABO和△DCO的外角
∴∠BOC=∠ABD+∠BAC,∠BOC=∠ACD+∠BDC
∴∠ABD+∠BAC=∠ACD+∠BDC
∵∠ABD=∠ACD
∴∠BAC=∠BDC
∵∠ACB=65°,AB=AC
∴∠ABC=∠ACB=65°
∴∠BAC=180°﹣∠ABC﹣∠ACB=180°﹣65°﹣65°=50°
∴∠BDC=∠BAC=50°

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目